CHAPITRE 1
Calcul arithmétique
- DIVISION EUCLIDIENNE ET CRITÈRES DE DIVISIBILITÉ1
- PRIORITÉS DE CALCUL2
Les critères de divisibilité
Définition
Définition
Divisibilité d’un nombre
➔ Si le reste de la division euclidienne de a par b est nul alors on dit que :
- b est un diviseur de a ;
- a est un multiple de b.
➔
Exemple
Exemple
|
Exemple
Exemple
Consigne :
5 est-il un diviseur de 30 ? Correction : 5×6=30, donc 5 est un diviseur de 30. |
Remarque
Remarque
Tout entier naturel admet au moins le nombre 1 et lui-même comme diviseurs.
|
Rappel
Rappel
Divisibilité d'un nombre
➔
- Tout nombre est divisible par 2 si son dernier chiffre est 0,2,4,6 ou 8.
- Tout nombre est divisible par 3 si la somme de ses chiffres est divisible par 3.
- Tout nombre est divisible par 4 si ses deux derniers chiffres forment un nombre multiple de 4.
- Tout nombre est divisible par 5 si son dernier chiffre est 0 ou 5.
- Tout nombre est divisible par 9 si la somme de ses chiffres est un multiple de 9.
- Tout nombre est divisible par 10 s’il se termine par 0.
➔
Exemple
Exemple
Consigne :
Trouvez quatre diviseurs de 150. Correction :
|
Rappel sur la division euclidienne
Rappel
Rappel
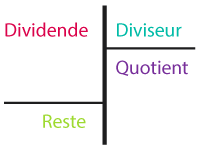
Division euclidienne
➔ Effectuer la division euclidienne d’un dividende par un diviseur, c’est trouver deux nombres appelés quotient et reste tels que :
- le dividende, le diviseur et le reste sont des entiers naturels ;
- dividende = diviseur × quotient + reste ;
- le reste est strictement inférieur au quotient.
➔
Exemple
Exemple
Consigne :
Quels sont le quotient et le reste de la division de 247 par 22 ? Correction :
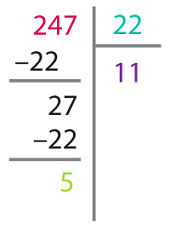 |
Remarque
Remarque
Attention ! Dans toute division, le diviseur n’est jamais égal à 0.
|
Utilisation des cookies
Lors de votre navigation sur ce site, des cookies nécessaires au bon fonctionnement et exemptés de consentement sont déposés.