CHAPITRE 11
Probabilités conditionnelles
- Cours
- Démonstration
- Formules
- Méthodes
Chapitre 11 - Probabilités conditionnelles
Cours
Probabilité conditionnelle
La probabilité conditionnelle que l’événement se réalise sachant que l’événement est réalisé est notée et est définie par .
Remarque : En réécrivant cette formule on obtient que .
Formule des probabilités totales
Sur un arbre de probabilité :
La somme des probabilités des branches issues d’un noeud est égale à 1.
La probabilité de l’événement à l’extrémité d’un chemin (l’intersection des événements rencontrés sur le chemin) est égale au produit des probabilités des branches composant ce chemin.
La probabilité d’un événement est égale à la somme des probabilités des chemins conduisant à cet événement. C’est la formule des probabilités totales.
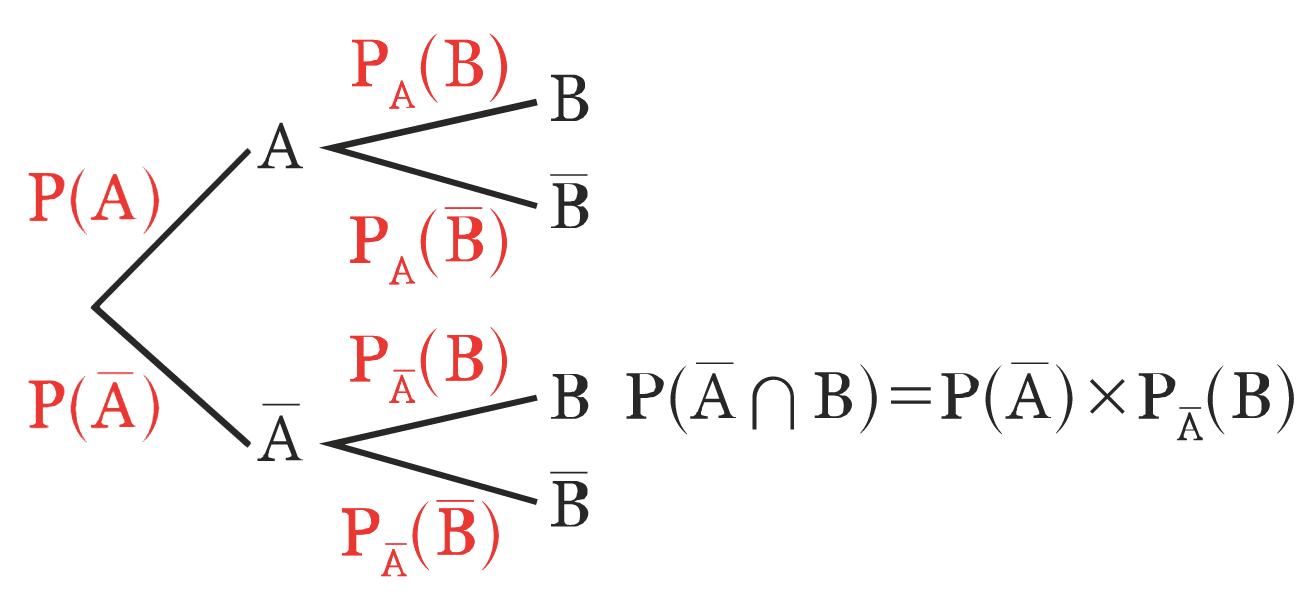
Événements indépendants
- Deux événements et sont dits indépendants lorsque .
Propriété : Deux événements et , tels que , sont indépendants si, et seulement si, .
Propriété : Si et sont indépendants alors et le sont aussi.
