CHAPITRE 10
Configurations géométriques
- Cours
- Démonstration
- Formules
Chapitre 10 - Configurations géométriques
Cours
Lieu géométrique
- Un lieu géométrique est un ensemble de points qui satisfont une même condition.
Exemple
L’ensemble des points vérifiant :
- est la médiatrice du segment .
- est une droite ou un morceau de droite suivant les valeurs possibles de .
Cercles
- Le cercle de centre et de rayon est l’ensemble des points vérifiants .
- Dans un repère orthonormé, une équation du cercle de centre et de rayon est donc .
Exemple
est une équation du cercle de centre et de rayon .
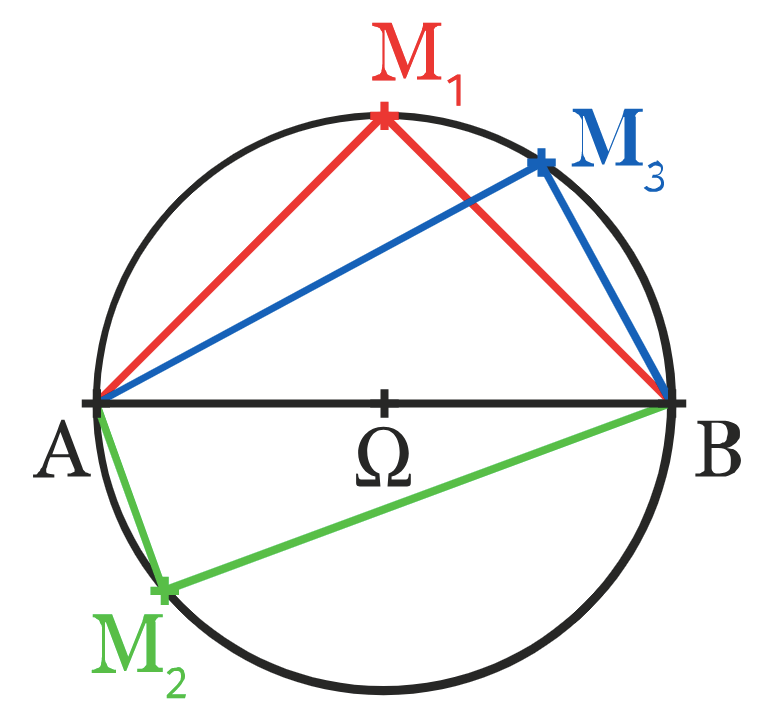
Le cercle de diamètre est l’ensemble des points vérifiants .
Propriété : Un cercle et une droite peuvent avoir , ou points d’intersections.
Triangles et centre de gravité
- Dans un triangle, la médiane issue d’un sommet est la droite passant par ce sommet et par le milieu du côté opposé.
- Les trois médianes d’un triangle sont concourantes et se coupent en , le centre de gravité du triangle.
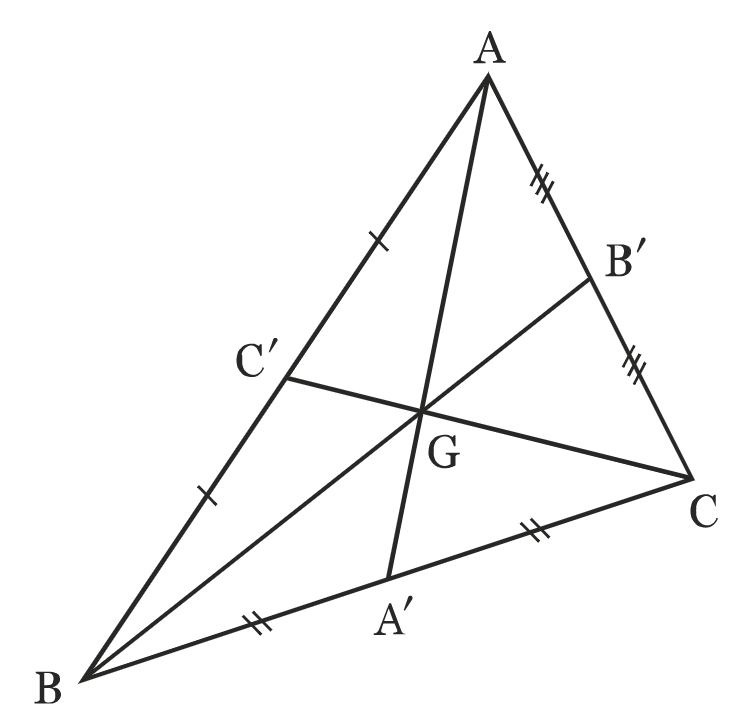
Propriétés :
- Le centre de gravité est l’unique point vérifiant .
- Le centre de gravité est situé aux deux tiers d’une médiane en partant du sommet dont elle est issue.
- Le centre de gravité est l’unique point vérifiant .
- Le centre de gravité est situé aux deux tiers d’une médiane en partant du sommet dont elle est issue.
Théorème de la médiane :
Soit un triangle. On note le milieu du segment . Alors :
- ;
- ;
-.
Soit un triangle. On note le milieu du segment . Alors :
- ;
- ;
-.
