CHAPITRE 9
Produit scalaire
- Cours
- Démonstration
- Formules
- Méthodes
Chapitre 9 - Produit scalaire
Cours
1Orthogonalité
1
Produit scalaire et orthogonalité
Les vecteurs AB et CD sont dits orthogonaux si les droites (AB) et (CD) sont perpendiculaires.
Les vecteurs u(−2 ;3) et v(6 ;4) sont orthogonaux car u⋅v=(−2)×6+3×4=0.
Propriété : Deux vecteurs u et v sont orthogonaux si, et seulement si, u⋅v=0.
Exemple :
Les vecteurs u(−2 ;3) et v(6 ;4) sont orthogonaux car u⋅v=(−2)×6+3×4=0.
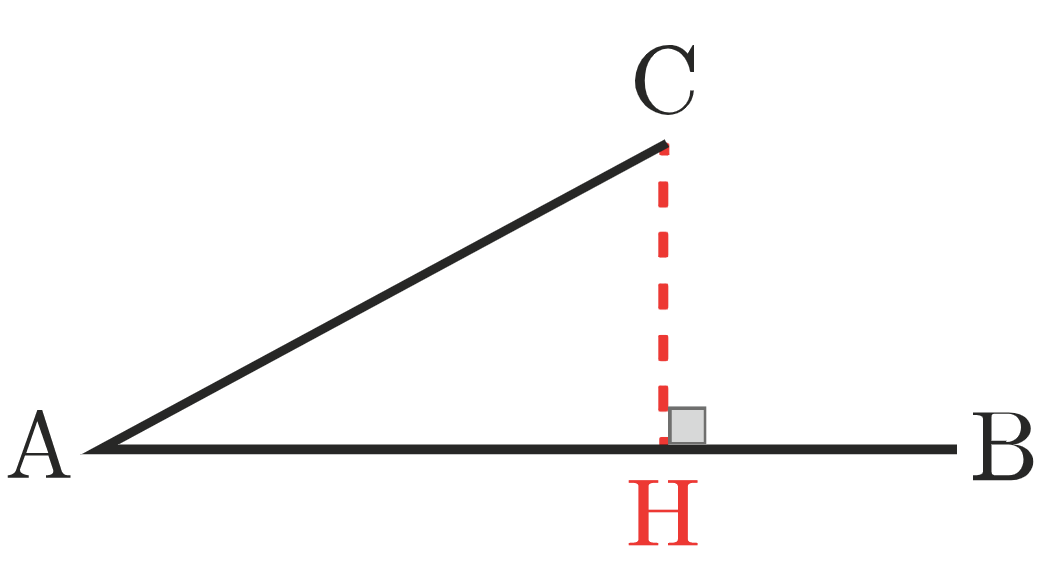
Projeté orthogonal
- Soient AB et AC deux vecteurs du plan.
- Soit H le projeté orthogonal du point C sur la droite (AB).
- Alors on a AB⋅AC=AB⋅AH.

2 Produit scalaire et droites
2
Vecteur normal et vecteur directeur
Un vecteur normal à une droite d est un vecteur non-nul orthogonal à un vecteur directeur de d, et donc à tous les vecteurs directeurs de d.
Un vecteur normal à la droite (AB) de vecteur directeur u(2 ;1) est, par exemple, v(−1 ;2) car u⋅v=2×(−1)+1×2=0.
Une droite admet une infinité de vecteurs directeurs et une infinité de vecteurs normaux.
Exemple :
Un vecteur normal à la droite (AB) de vecteur directeur u(2 ;1) est, par exemple, v(−1 ;2) car u⋅v=2×(−1)+1×2=0.
Attention
Propriété : Deux droites du plan sont perpendiculaires si, et seulement si, un vecteur normal de l’une est orthogonal à un vecteur normal de l’autre.
Équations cartésiennes
Exemple :
La droite d’équation 2x+3y+6=0 admet n(23) pour vecteur normal.
Remarque : Une telle droite admet u(−ba) pour vecteur directeur.
Utilisation des cookies
Lors de votre navigation sur ce site, des cookies nécessaires au bon fonctionnement et exemptés de consentement sont déposés.