CHAPITRE 8
Fonctions trigonométriques
- Cours
Chapitre 8 - Fonctions trigonométriques
Cours
1Fonction cosinus
1
Définition et propriétés
La fonction cosinus est la fonction qui, à tout réel , associe .
Propriétés :
La fonction cosinus est paire (c’est à dire que pour tout réel , .
La fonction cosinus est (c’est à dire que pour tout , ).
Courbe représentative
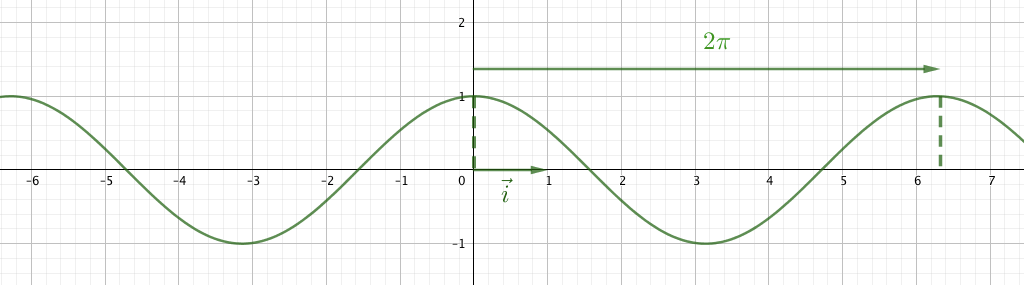
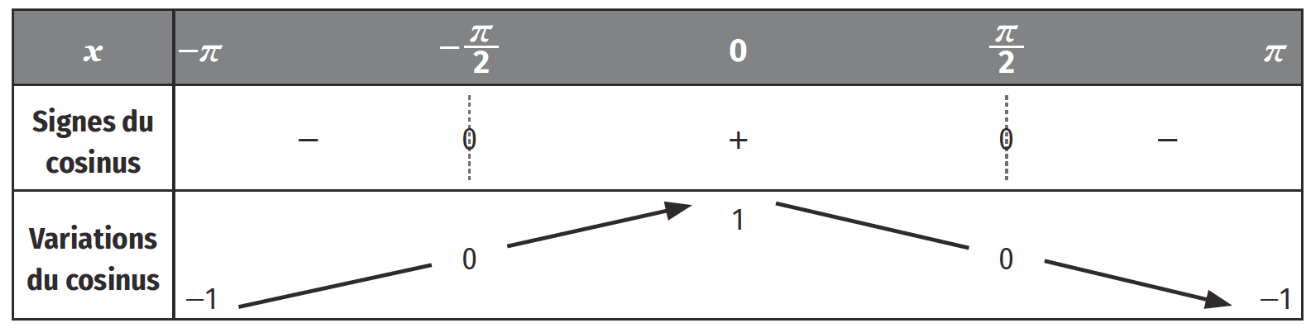
Tableaux de signes et de variations
La fonction cosinus étant , on peut restreindre son étude sur l’intervalle .
2 Fonction sinus
2
Définition et propriétés
La fonction sinus est la fonction qui, à tout réel , associe .
Propriétés :
La fonction cosinus est impaire (c’est à dire que pour tout réel , .
La fonction sinus est (c’est à dire que pour tout , ).
La fonction sinus est (c’est à dire que pour tout , ).
Courbe représentative
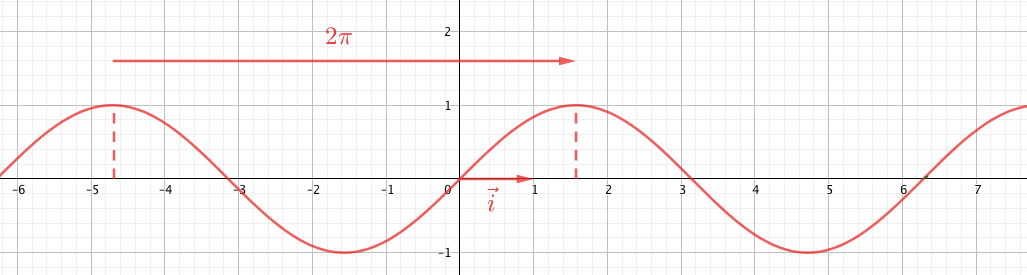
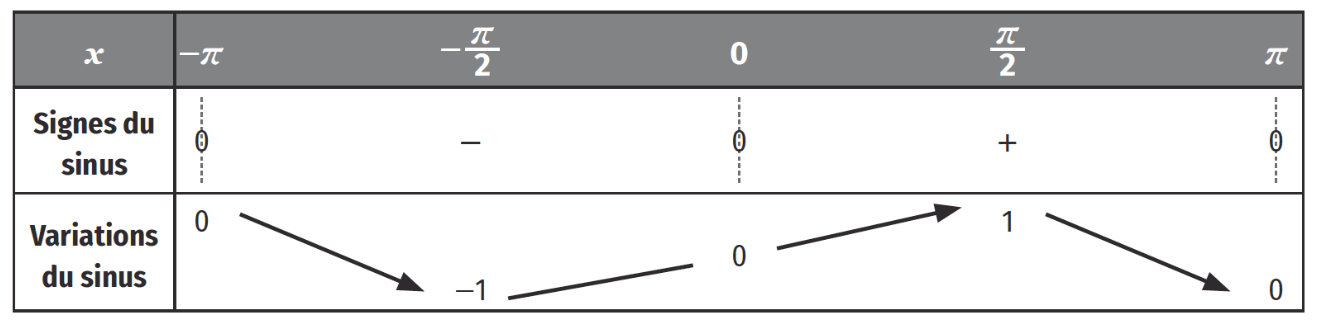
Tableaux de signes et de variations
La fonction sinus étant , on peut restreindre son étude sur l’intervalle .
