CHAPITRE 7
Trigonométrie
- Cours
- Démonstration
- Formules
Chapitre 7 - Trigonométrie
Cours
Cercle trigonométrique
Dans un repère orthonormé (O ;I,J), le cercle trigonométrique est le cercle de centre O et de rayon 1 orienté dans le sens inverse des aiguilles d’une montre, appelé sens direct ou bien encore sens trigonométrique.

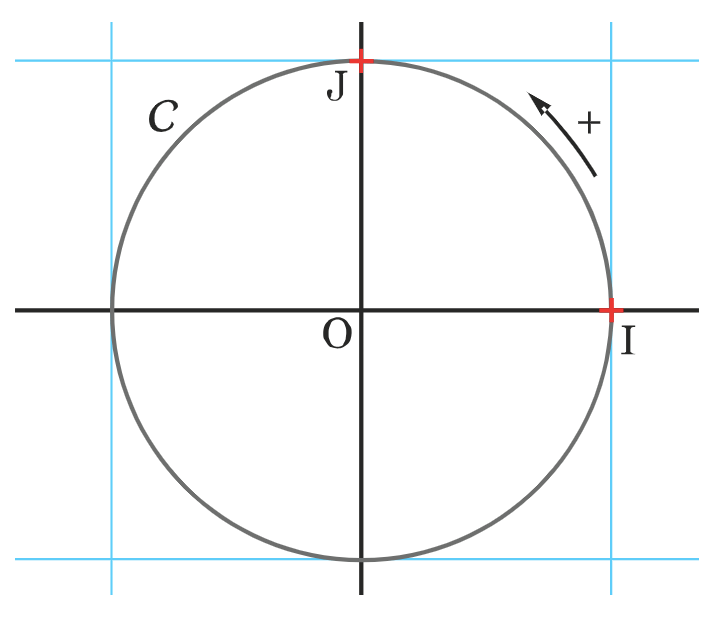


Remarque : Le sens contraire du sens direct est appelé sens indirect ou bien encore sens anti-trigonométrique.
Radian
On enroule autour du cercle trigonométrique la droite numérique. On fait ainsi correspondre chaque réel x à un point du cercle trigonométrique.

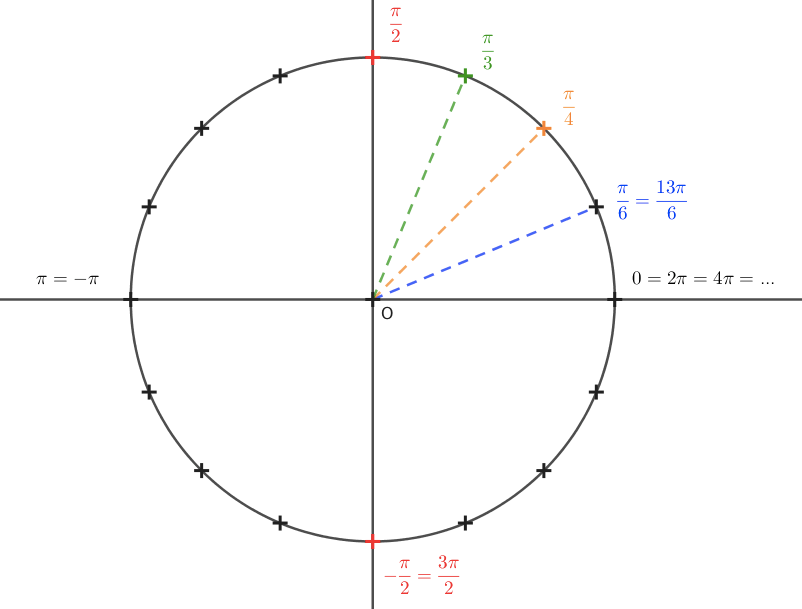 On place un angle au centre du cercle trigonométrique et on fait correspondre un de ses côtés avec la demi-droite des abscisses positives. Le deuxième côté de l’angle intersecte alors le cercle trigonométrique en un point.
On place un angle au centre du cercle trigonométrique et on fait correspondre un de ses côtés avec la demi-droite des abscisses positives. Le deuxième côté de l’angle intersecte alors le cercle trigonométrique en un point.

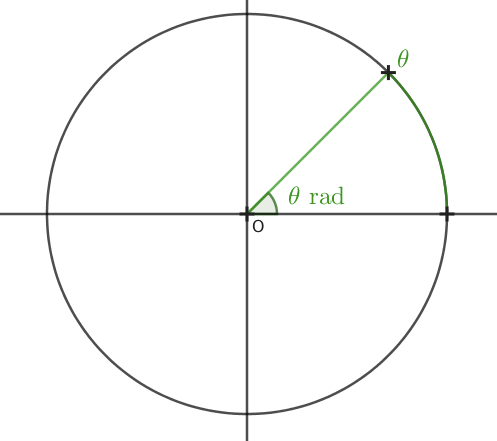
Dans la figure ci-dessus, l’angle intersecte le cercle trigonométrique en 4π. On peut donc écrire θ=4π rad.
Un angle mesurant 73π rad mesure aussi 73π+1×2π=717π rad, il mesure aussi 73π+111×2π=71557π rad, ou bien encore 73π−12×2π=−7165π rad.




Exemple :
Dans la figure ci-dessus, l’angle intersecte le cercle trigonométrique en 4π. On peut donc écrire θ=4π rad.
Propriété : Un angle ne possède pas qu’une seule mesure en radian.
Deux mesures en radian θ et θ‘ correspondent au même angle si, et seulement si, il existe k∈Z tel que θ=θ‘+k×2π.
Exemple :
Un angle mesurant 73π rad mesure aussi 73π+1×2π=717π rad, il mesure aussi 73π+111×2π=71557π rad, ou bien encore 73π−12×2π=−7165π rad.
Cosinus et sinus
On considère un réel x ayant pour point image le point M sur le cercle trigonométrique.
L’abscisse du point M est appelée cosinus de x. On la note cos(x).
L’ordonnée du point M est appelée sinus de x. On la note sin(x).

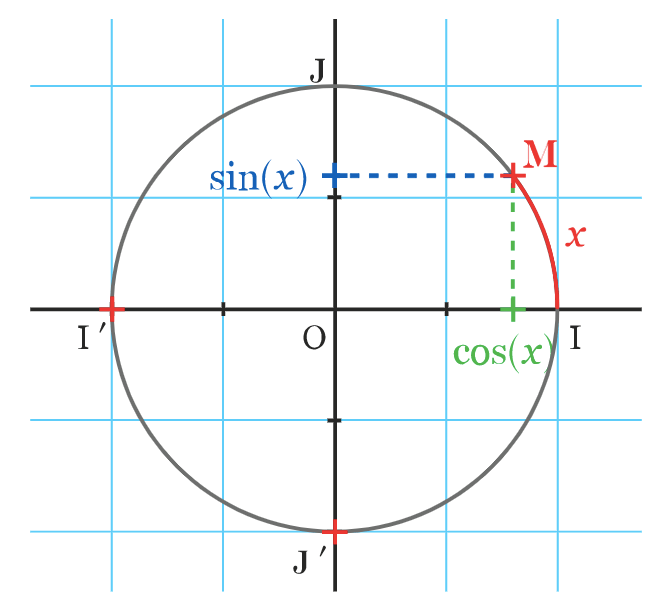

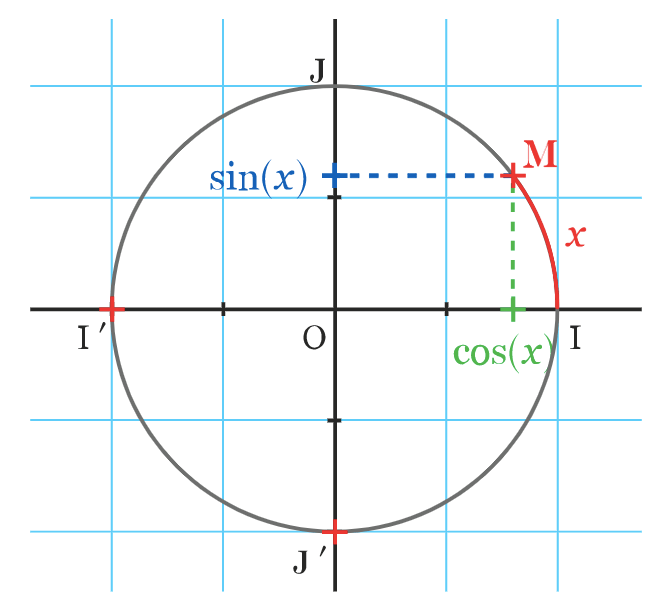
Propriété - Pour tout nombre x, on a :
−1⩽cos(x)⩽1
−1⩽sin(x)⩽1
cos2(x)+sin2(x)=1
Utilisation des cookies
Lors de votre navigation sur ce site, des cookies nécessaires au bon fonctionnement et exemptés de consentement sont déposés.