CHAPITRE 5
Applications de la dérivation
- Cours
- Démonstration
- Méthodes
Chapitre 5 - Application de la dérivation
Cours
Sens de variation d'une fonction
Soient f une fonction dérivable sur un intervalle I et f‘ sa fonction dérivée.
f est croissante sur I si, et seulement si, f‘ est positive sur I.
f est décroissante sur I si, et seulement si, f‘ est négative sur I.
f est constante sur I si, et seulement si, f‘ est nulle sur I.
Extremums d'une fonction
f(c) est un maximum local (respectivement un minimum) de la fonction f au voisinage de c si, et seulement si, il existe deux réels a et b tels que c∈]a;b[ et, pour tout réel x∈]a;b[, f(x)⩽f(c) (respectivement f(x)⩾f(c)).

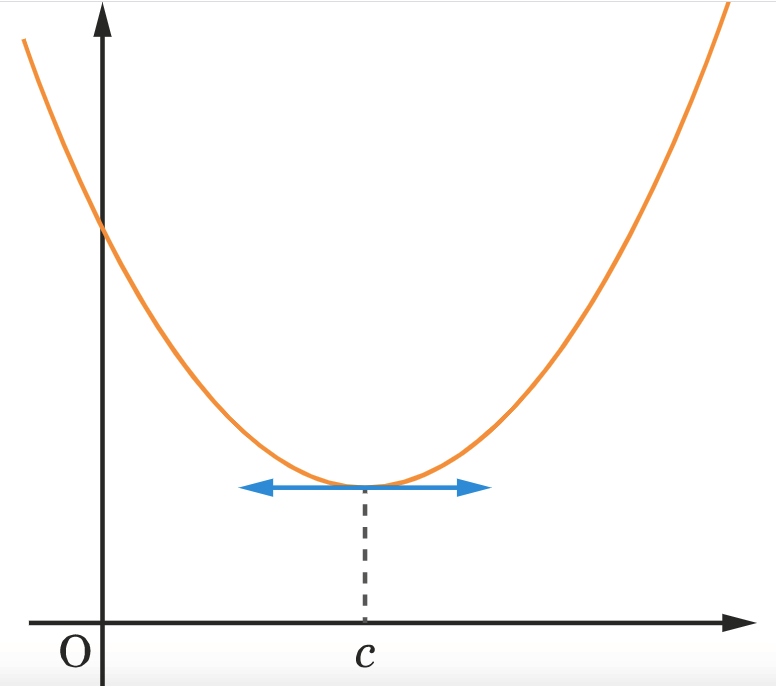

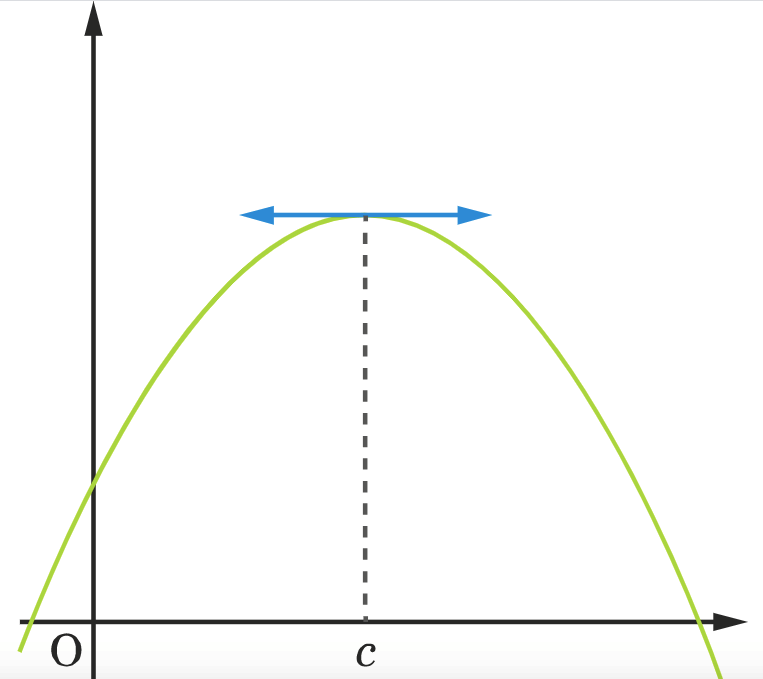
Propriété : f admet un extremum local en c si, et seulement si, f‘ s’annule en c en changeant de signe.




Utilisation des cookies
Lors de votre navigation sur ce site, des cookies nécessaires au bon fonctionnement et exemptés de consentement sont déposés.