CHAPITRE 8
Équations de droites
- Cours
- Démonstration
- Formules
- Méthodes
Chapitre 8 - Équations de droites
Cours
Vecteur directeur
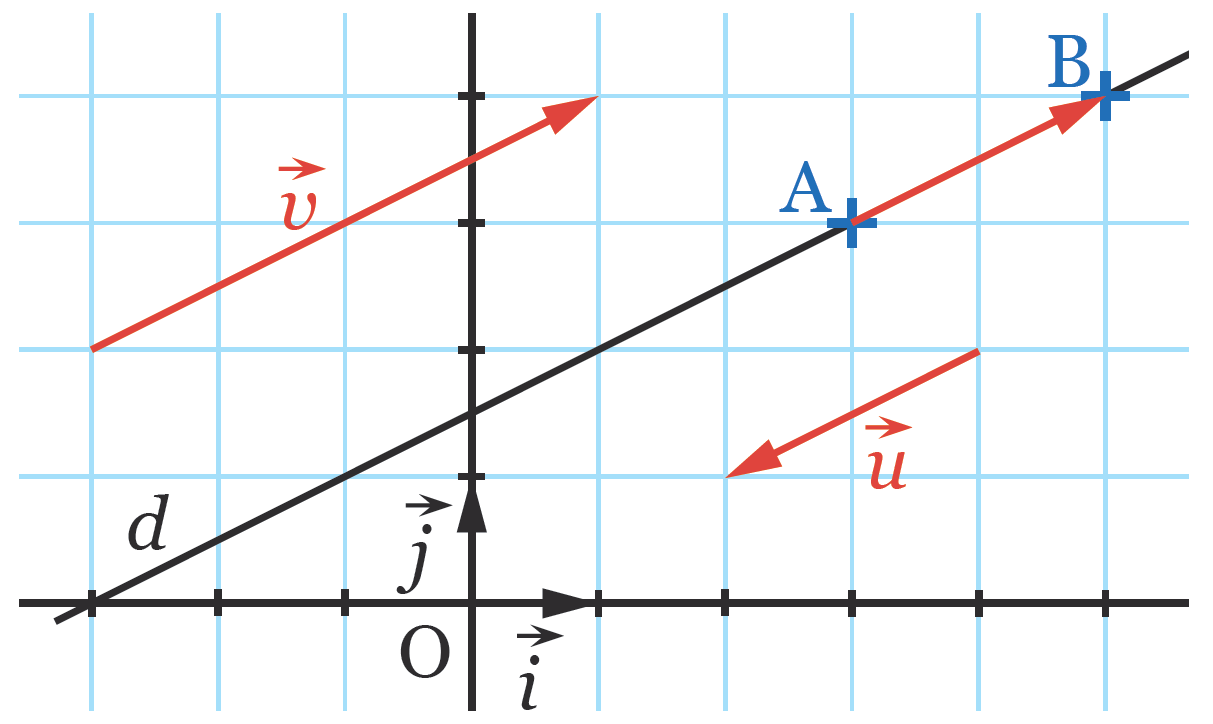
Un vecteur directeur d’une droite d est un représentant d’un vecteur AB avec A et B deux points distincts de d.
Dans la figure ci-dessous, les vecteurs AB, u et v sont des vecteurs directeurs de la droite d.

Exemple
Dans la figure ci-dessous, les vecteurs AB, u et v sont des vecteurs directeurs de la droite d.


Équation cartésienne
Une équation cartésienne de droite est une équation de la forme ax+by+c=0.
3x+2y+1=0 et 6x+4y+2=0 sont deux équations cartésiennes d’une même droite. Un vecteur directeur de cette droite a pour coordonnées (−2 ;3) par exemple. Un autre vecteur directeur de cette droite a pour coordonnées (−4 ;6).
Remarque : Il existe une infinité d’équations cartésiennes d’une même droite.
Propriété : Si une droite a pour équation cartésienne ax+by+c=0 alors un vecteur directeur de cette droite a pour coordonnées (−b;a).
Exemple
3x+2y+1=0 et 6x+4y+2=0 sont deux équations cartésiennes d’une même droite. Un vecteur directeur de cette droite a pour coordonnées (−2 ;3) par exemple. Un autre vecteur directeur de cette droite a pour coordonnées (−4 ;6).
Équation réduite
Une équation réduite de droite est une équation de la forme y=mx+p.
Remarque : Une droite verticale n’admet pas d’équation réduite. Une droite non-verticale admet une seule et unique équation réduite.
- Le nombre m est appelé le coefficient directeur de la droite.
- Le nombre p est appelé l’ordonnée à l’origine de la droite.
Exemple
Une droite d’équation cartésienne 6x+3y−3=0 a pour équation réduite y=−2x+1. Le coefficient directeur de cette droite vaut −2, et l’ordonnée à l’origine de cette droite vaut 1.
Positions relatives de droites

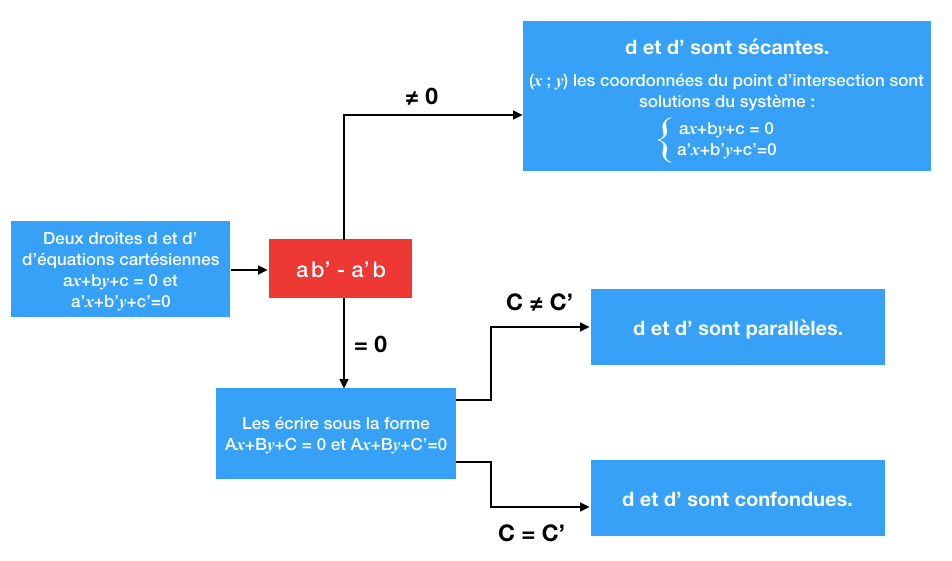
Exemple 1
Les droites d’équation x+2y−7=0 et 2x+y−8=0 ne sont pas parallèles car 1×1−2×2=−3=0. Les coordonnées de leur point d’intersection sont solutions du système {2x+2y−7=02x+y−8=0, c’est à dire {x=3y=2.
Exemple 2
Les droites d’équation x+3y+4=0 et 2x+6y−2=0 sont parallèles car 1×6−2×3=0. On peut diviser la deuxième équation par 2 pour obtenir une nouvelle équation cartésienne de la droite : x+3y−1=0. On a 4=−1, donc ces deux droites ne sont pas confondues.
Utilisation des cookies
Lors de votre navigation sur ce site, des cookies nécessaires au bon fonctionnement et exemptés de consentement sont déposés.