CHAPITRE 5
Repérage et configuration dans le plan
Accueil > Mathématiques Seconde > Chapitre 5 - Repérage et configuration dans le plan - fiche de cours
- Cours
- Démonstration
- Formules
- Méthodes
Chapitre 5 - Repérage et configuration dans le plan
Cours
1Géométrie analytique
1
Repère du plan
Coordonnées d'un point
- Dans un repère, chaque point M est associé à un unique couple de réels (x ;y). On appelle ce couple (x;y) les coordonnées du point M.
- Le nombre x est appelé l’abscisse du point M.
- Le nombre y est appelé l’ordonnée du point M.
Exemple

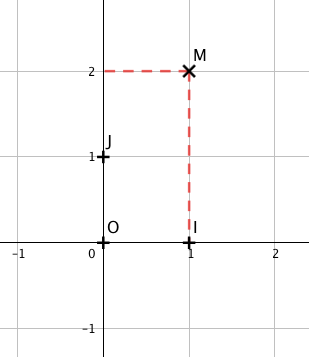
Sur cette figure le repère (O ; I, J) est orthonormé.
❯ O est l’origine du repère ;
❯ (OI) est l’axe des abscisses ;
❯ (OJ) est l’axe des ordonnées.
Le point M admet pour coordonnées (1 ;2).
Points alignés
Trois points A, B et C sont alignés dans cet ordre si et seulement AC=AB+BC.

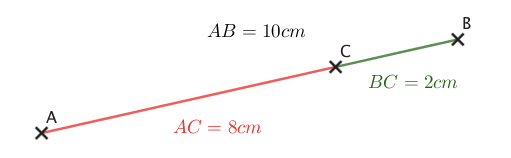
Si AC=8 cm, AB=10 cm et BC=2 cm alors A, C et B sont alignés dans cet ordre car AB=AC+BC.
Exemple


Si AC=8 cm, AB=10 cm et BC=2 cm alors A, C et B sont alignés dans cet ordre car AB=AC+BC.
2 Géométrie descriptive
2
Projeté orthogonal
Le projeté orthogonal d’un point M sur une droite d est le point M’ tel que (MM’)⊥ d.

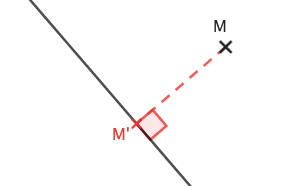


Propriété : Le projeté orthogonal d’un point M sur une droite Δ est le point de Δ le plus proche de M.
Géométrie du triangle

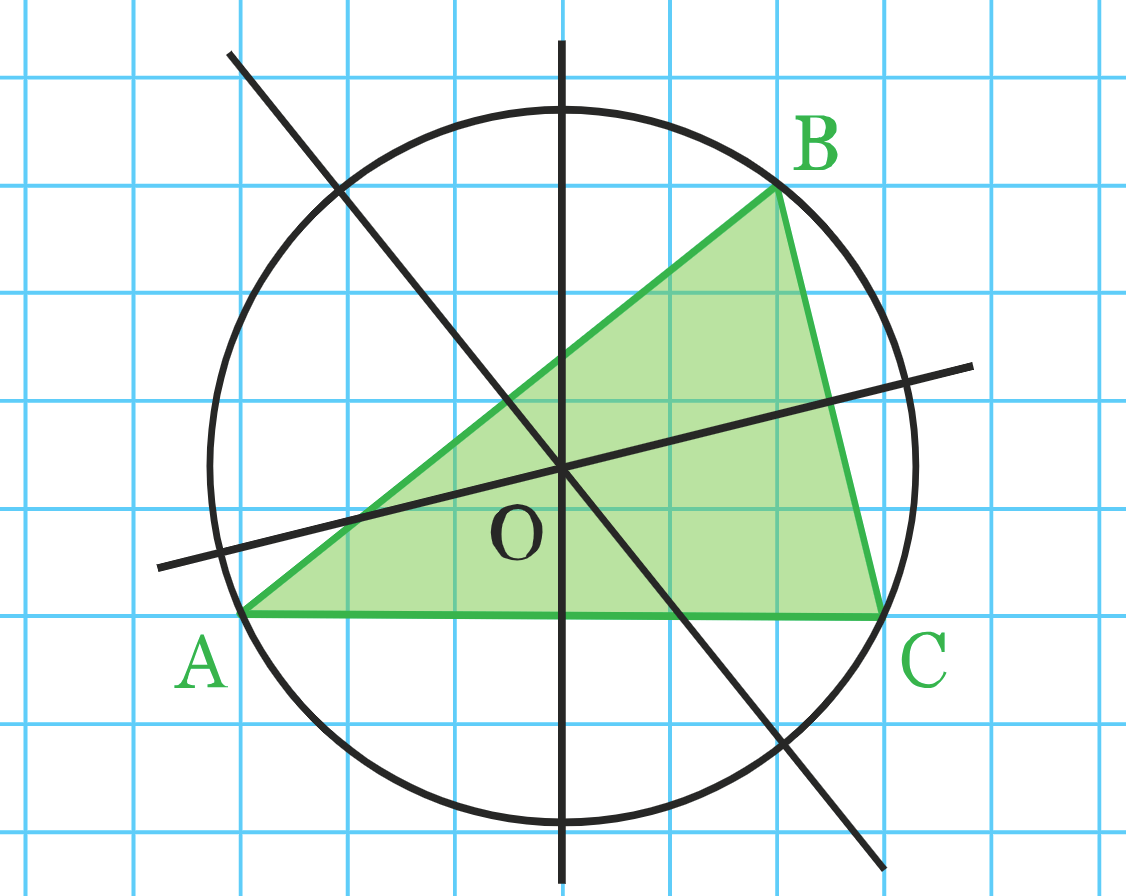

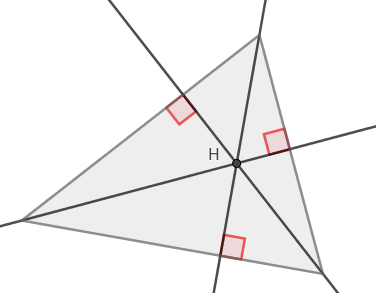
Propriété :
Dans un triangle équilatéral, les hauteurs et les médiatrices sont confondues. Le centre du cercle circonscrit et l’orthocentre le sont donc aussi.
Dans un triangle équilatéral, les hauteurs et les médiatrices sont confondues. Le centre du cercle circonscrit et l’orthocentre le sont donc aussi.
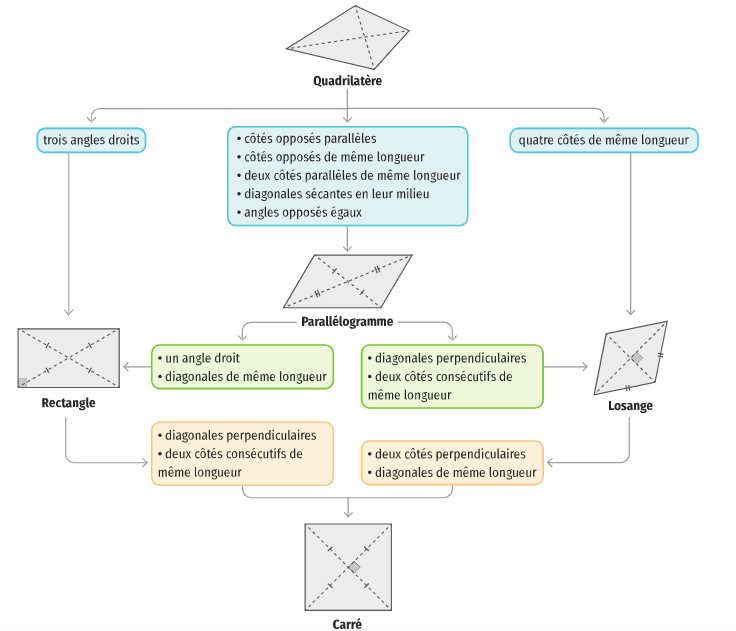
Géométrie des quadrilatères

Utilisation des cookies
Lors de votre navigation sur ce site, des cookies nécessaires au bon fonctionnement et exemptés de consentement sont déposés.