CHAPITRE 4
Fonctions de référence
- Cours
- Démonstration
- Méthodes
Chapitre 4 - Fonctions de référence
Cours
1Fonction carré
1
Définition et propriétés
La fonction carré est la fonction définie pour tout réel par
Propriétés de la fonction carré :
La fonction carré est paire : pour tout ,
La fonction carré est positive : pour tout , .
Courbe représentative
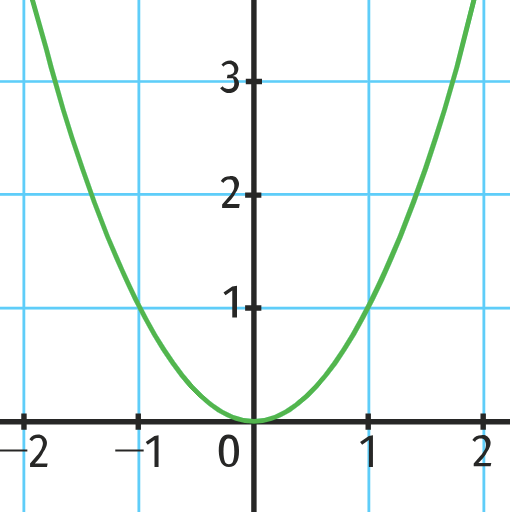
La courbe représentative de la fonction carré est une parabole tournée vers le haut.
Variations
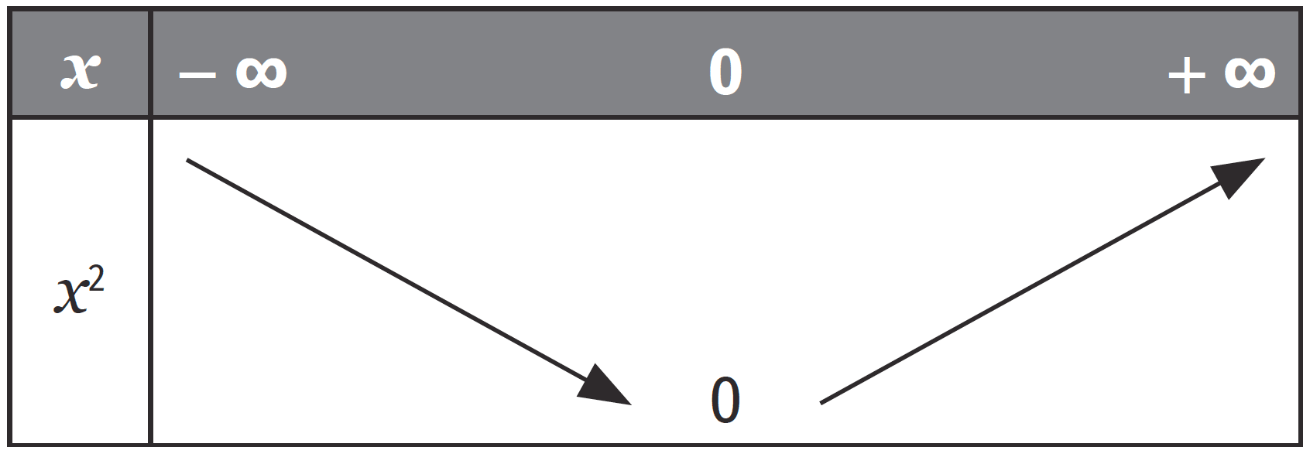
Résolution d'équation
Sur , l'équation ...
N'admet aucune solution si .
Admet une unique solution si , cette solution est .
Deux solutions si , ces solutions sont et
Résolution d'inéquation
Sur , l'inéquation ...
N'admet aucune solution si .
Admet une unique solution si , cette solution est .
Admet pour solutions les éléments de l'intervalle
2Fonction racine carrée
2
Définition et propriétés
La fonction racine carrée est la fonction définie pour par
Propriétés de la fonction racine carré :
La fonction racine carrée est positive : pour tout , .
Pour tous réels positif et ,
Pour tous réels positif et positif non nul,
Courbe représentative
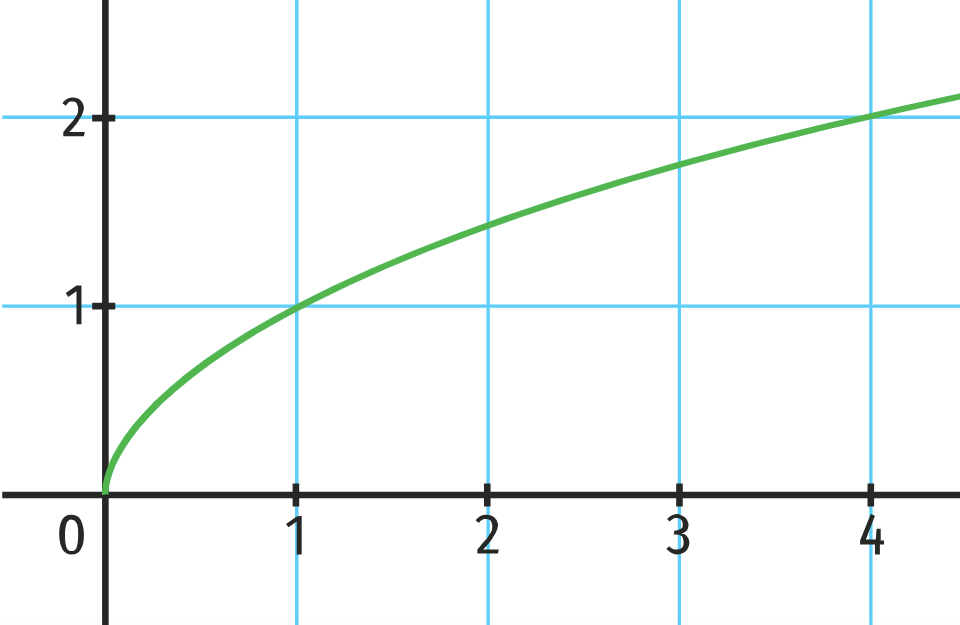
Variations
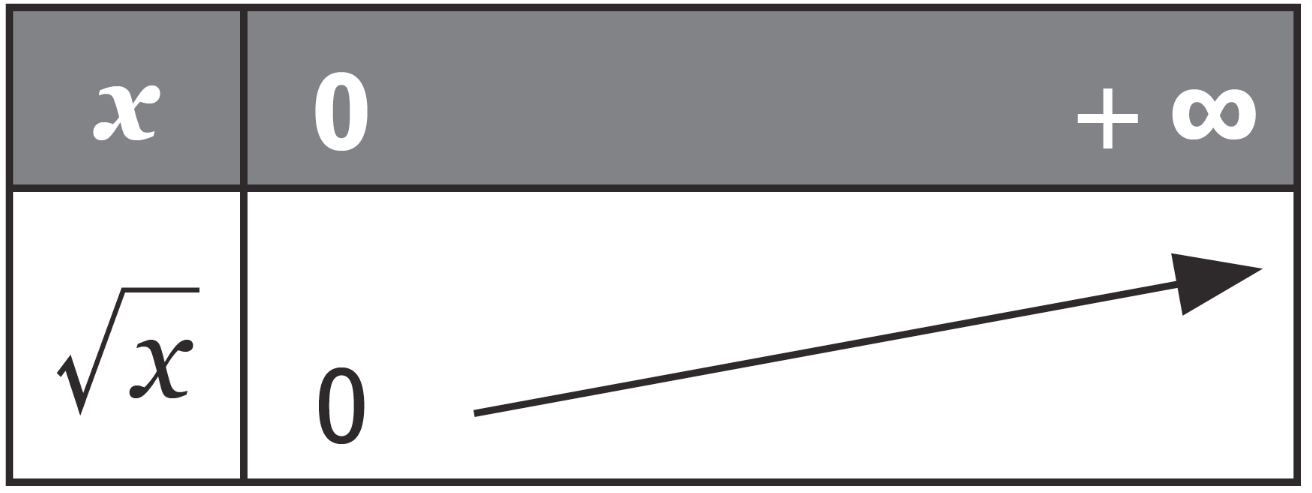
3Fonction inverse
3
Définition et propriétés
La fonction inverse est la fonction définie pour tout réel par
Propriétés de la fonction inverse :
La fonction inverse est impaire : pour tout ,
La fonction inverse ne s'annule jamais sur son ensemble de définition.
Courbe représentative
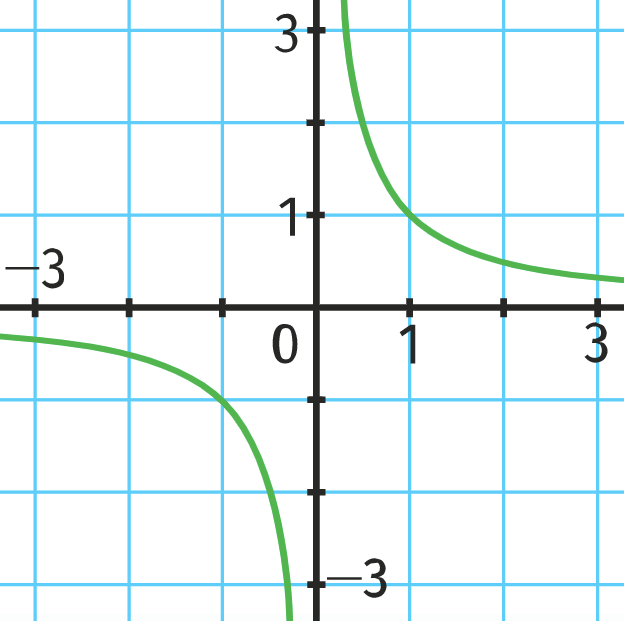
La courbe représentative de la fonction inverse est une hyperbole.
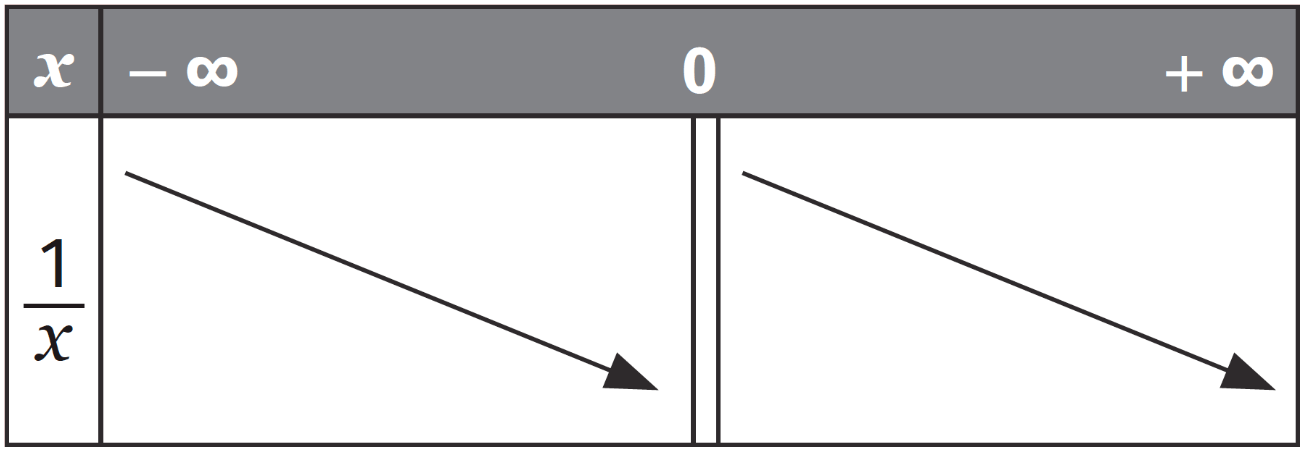
Variations
4Fonction cube
4
Définition et propriété
La fonction cube est la fonction définie pour tout réel par
Propriété de la fonction cube :
La fonction cube est impaire : pour tout ,
Courbe représentative
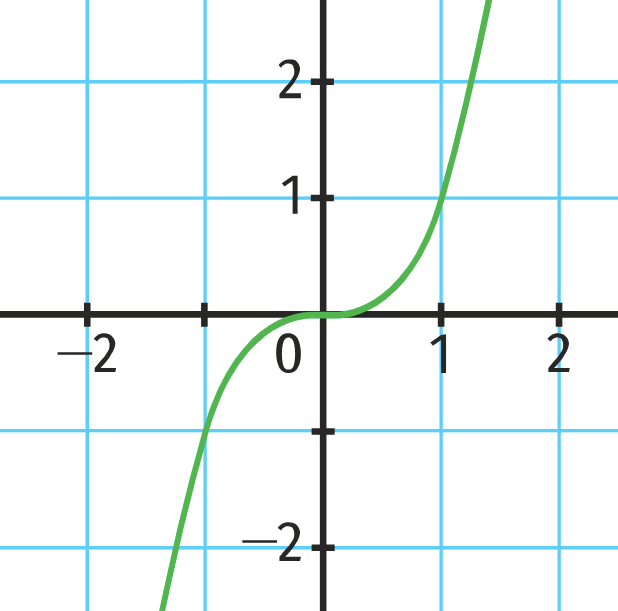
Variations
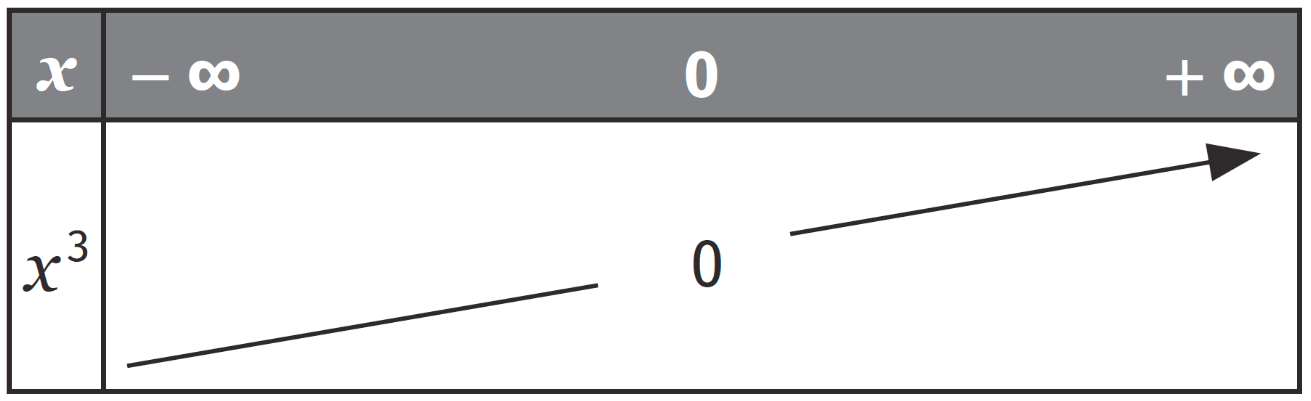
5Positions relatives
5
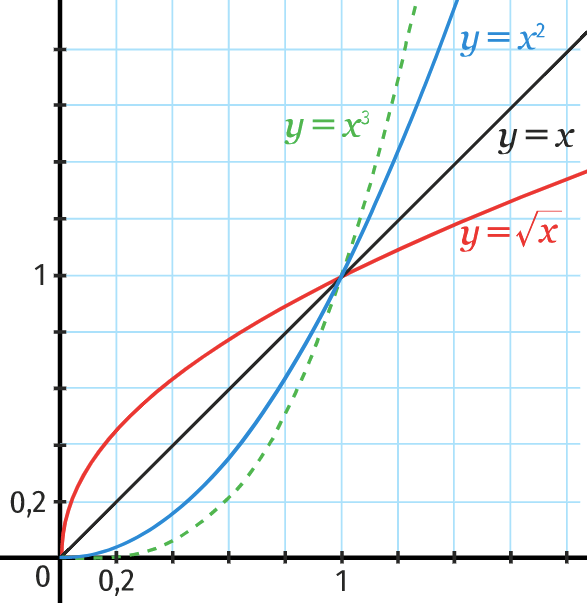
Positions relatives des courbes sur
Graphiquement
