CHAPITRE 3
Fonctions affines
- Cours
- Démonstration
- Formules
- Méthodes
Chapitre 3 - Fonctions affines
Cours
1Généralités sur les fonctions affines
1
Fonctions affines, linéaires et constantes
Une fonction f définie sur R est dite affine lorsqu’il existe deux réels m et p tels que, pour tout x∈R,
f(x)=mx+p.
Si m=0, alors la fonction f est une fonction constante.
Si p=0, alors la fonction f est une fonction linéaire.
Exemples :
- f(x)=−3x+1 est une fonction affine avec m=−3 et p=1.
f(x)=−3=0×x−3 est une fonction affine avec m=0 et p=−3. Comme m=0, la fonction est constante.
f(x)=2x=2×x+0 est une fonction affine avec m=2 et p=0. Comme p=0 la fonction est linéaire.
Coefficient directeur m
Le nombre m s'appelle le coefficient directeur de la fonction f.
Exemple :
- Le coefficient directeur de
f(x)=−4x−1 est égal à −4.
Formule de calcul :
m=b−af(b)−f(a)
Ordonnée à l'origine p
Le nombre p s'appelle l'ordonnée à l'origine de la fonction f.
Exemple :
- L'ordonnée à l'origine de la fonction
f(x)=−4x−1 est égal à −1.
Formule de calcul :
p=f(a)−ma
Représentation graphique
Dans un repère orthonormé (O ;I,J), la courbe représentative d'une fonction f affine est une droite non parallèle à l'axe des ordonnées.
La pente de cette droite est égale au coefficient directeur de la fonction f.
L'ordonnée à l'origine de la fonction f correspond à l'ordonnée à laquelle la droite coupe l'axe des ordonnées.
L'ordonnée à l'origine de la fonction f correspond à l'ordonnée à laquelle la droite coupe l'axe des ordonnées.
Remarque : La représentation graphique d'une fonction linéaire est une droite passant par l'origine.
2 Étude d’une fonction affine
2
Parité
Variations
Exemples :
- f(x)=3x+1 est croissante car m=3>0.
f(x)=−1,5x−4 est décroissante car m=−1,5<0.
Signes
Si m>0
Alors f(x)>0⇔x>−mp.

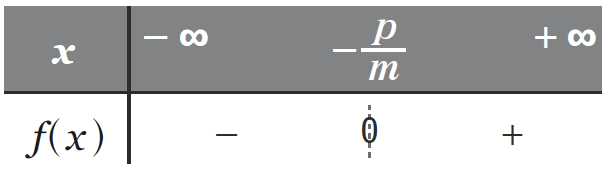

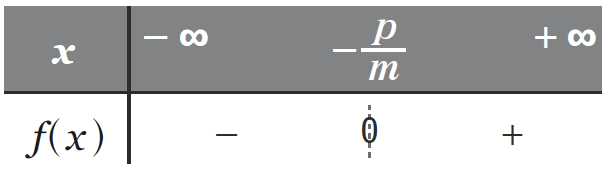
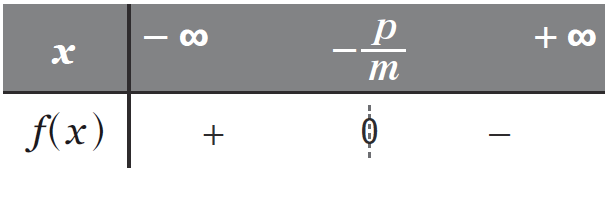
Si m<0
Alors f(x)>0⇔x<−mp.



Utilisation des cookies
Lors de votre navigation sur ce site, des cookies nécessaires au bon fonctionnement et exemptés de consentement sont déposés.