CHAPITRE 2
Variations de fonctions
- Cours
- Méthodes
Chapitre 2 - Variations de fonctions
Cours
Fonction décroissante
Une fonction f est décroissante sur un intervalle I si pour tout réels a<b de I on a f(a)⩾f(b).




Fonction croissante
Une fonction f est croissante sur un intervalle I si pour tout réels a<b de I on a f(a)⩽f(b).




Fonction strictement croissante ou décroissante
Une fonction f est strictement croissante (respectivement strictement décroissante) sur un intervalle I si pour tout réels a<b de I on a f(a)<f(b) (respectivement f(a)>f(b)).
La fonction f est strictement croissante (et donc croissante) sur [1;3]. La fonction g est croissante sur [1;3] mais n’est pas strictement croissante sur cet intervalle car elle est constante sur [2;2,5].

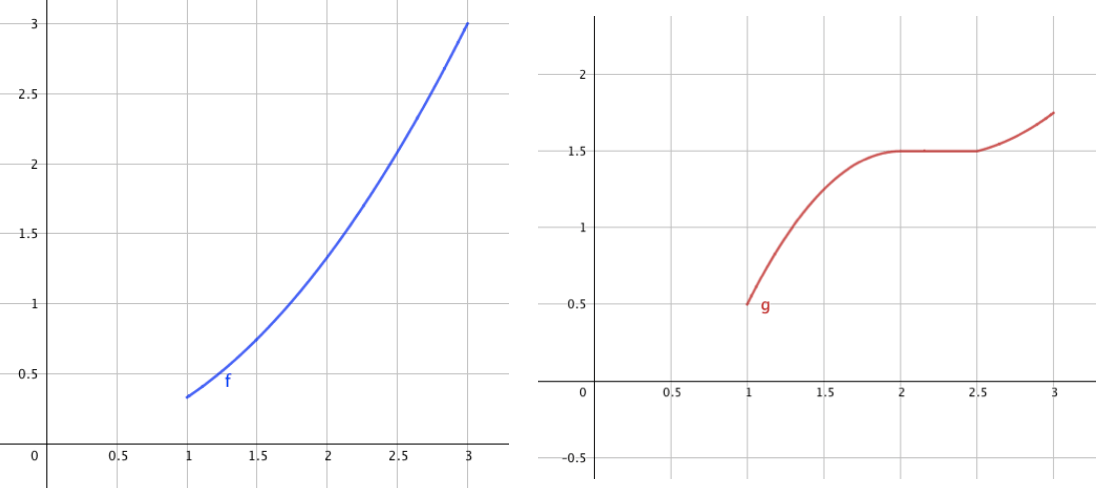
Exemple
La fonction f est strictement croissante (et donc croissante) sur [1;3]. La fonction g est croissante sur [1;3] mais n’est pas strictement croissante sur cet intervalle car elle est constante sur [2;2,5].


Monotonie
Une fonction f est monotone sur un intervalle I si elle soit croissante, soit décroissante sur cet intervalle.
La fonction f est monotone sur l’intervalle [0;2] mais pas monotone sur l’intervalle [0;4] : elle est croissante puis décroissante sur cet intervalle.

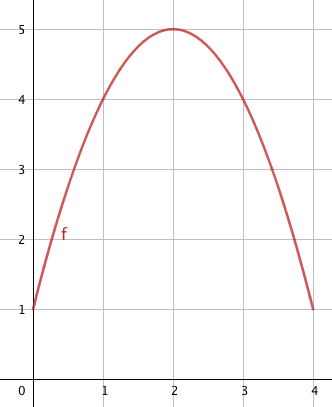
Exemple
La fonction f est monotone sur l’intervalle [0;2] mais pas monotone sur l’intervalle [0;4] : elle est croissante puis décroissante sur cet intervalle.


Extremums


Remarque : Une fonction n’admet pas obligatoirement un minimum ou un maximum. Par exemple la fonction f(x)=x n’admet ni maximum, ni minimum sur R.
Utilisation des cookies
Lors de votre navigation sur ce site, des cookies nécessaires au bon fonctionnement et exemptés de consentement sont déposés.