CHAPITRE 1
Généralités sur les fonctions
- Cours
- Méthodes
Chapitre 1 - Généralités sur les fonctions
Cours
1Vocabulaire des fonctions
1
Notion de fonction
Une fonction f sur un ensemble de réels D est un objet mathématique associant à chaque réel x∈D un unique réel y.
On note f(x)=y (ce qui se lit « f de x égal y »).




L’ensemble D est appelé l’ensemble de définition de f.
Soit f la fonction qui à la longueur du côté d’un carré associe l’aire de ce carré. On a f(2)=4 car l’aire d’un carré de côté 2 vaut 4. L’ensemble de définition de cette fonction est l’intervalle [0;+∞[.
On note f(x)=y (ce qui se lit « f de x égal y »).




L’ensemble D est appelé l’ensemble de définition de f.
Exemple
Soit f la fonction qui à la longueur du côté d’un carré associe l’aire de ce carré. On a f(2)=4 car l’aire d’un carré de côté 2 vaut 4. L’ensemble de définition de cette fonction est l’intervalle [0;+∞[.
Images et antécédents
Si f(x)=y alors :
Soit f la fonction qui au numéro d’un mois de l’année (par exemple le nombre 1 correspond au mois de janvier, le nombre 2 correspond au mois de février, etc. ) associe le nombre de jours de ce mois lors d’une année non bissextile.
L’image de 1 par la fonction f est 31. Donc 1 est un antécédent de 31 par la fonction f. Mais 31 a d’autres antécédents : 3 par exemple, ou bien encore 5 car janvier n’est pas le seul mois à être composé de 31 jours.
- y est appelé l’image de x par f.
- x est appelé un antécédent de y par f.
Remarque importante : Un antécédent n’a toujours qu’une seule image mais une image peut avoir plusieurs antécédents.
Exemple
Soit f la fonction qui au numéro d’un mois de l’année (par exemple le nombre 1 correspond au mois de janvier, le nombre 2 correspond au mois de février, etc. ) associe le nombre de jours de ce mois lors d’une année non bissextile.
L’image de 1 par la fonction f est 31. Donc 1 est un antécédent de 31 par la fonction f. Mais 31 a d’autres antécédents : 3 par exemple, ou bien encore 5 car janvier n’est pas le seul mois à être composé de 31 jours.
Expression algébrique
On peut définir une fonction en donnant son expression algébrique.
Par exemple, f(x)=x2+x+1 est l’expression algébrique d’une fonction f.
L’expression algébrique d’une fonction permet de connaître l’image de n’importe quel antécédent. Elle permet d’avoir une description complète de la fonction contrairement aux courbes et aux tableaux.
Par exemple, f(x)=x2+x+1 est l’expression algébrique d’une fonction f.
L’expression algébrique d’une fonction permet de connaître l’image de n’importe quel antécédent. Elle permet d’avoir une description complète de la fonction contrairement aux courbes et aux tableaux.
Tableau de valeurs
On peut définir une fonction f en donnant un tableau de valeurs.
On donne explicitement les images associées à différentes valeurs de x.
Un tableau de valeurs ne permet pas d’avoir une description complète de la fonction : on ne connaît les images que d’un nombre fini d’antécédents.
| x | –1 | 0 | 5 | 10 |
|---|---|---|---|---|
| f(x) | 0 | 2 | 3 | 2 |
Un tableau de valeurs ne permet pas d’avoir une description complète de la fonction : on ne connaît les images que d’un nombre fini d’antécédents.
Courbe représentative
On peut définir une fonction f en traçant sa courbe représentative.
On trace dans le plan l’ensemble des points A(x;y) tels que y=f(x).


Un tableau de valeurs ne permet pas d’avoir une description complète de la fonction : on ne connaît les images des antécédents que sur l’intervalle sur lequel la fonction est dessinée. La lecture des images et des antécédents peut aussi se révéler peu précise.


Un tableau de valeurs ne permet pas d’avoir une description complète de la fonction : on ne connaît les images des antécédents que sur l’intervalle sur lequel la fonction est dessinée. La lecture des images et des antécédents peut aussi se révéler peu précise.
2Parité
2
Fonction paire
Une fonction f définie sur un intervalle I est paire si pour tout x∈I, f(−x)=f(x).
La courbe d’une fonction paire est symétrique par rapport à l’axe des ordonnées.

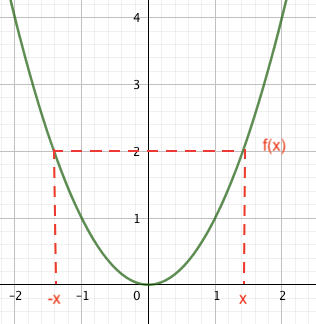
La courbe d’une fonction paire est symétrique par rapport à l’axe des ordonnées.


Fonction impaire
Une fonction f définie sur un intervalle I est impaire si pour tout x∈I, f(−x)=−f(x).
La courbe d’une fonction paire est symétrique par rapport à l’origine du repère.

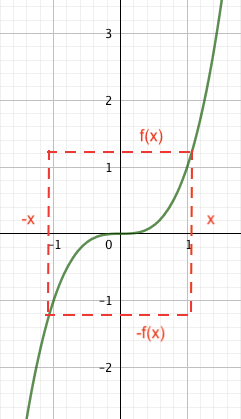
La courbe d’une fonction paire est symétrique par rapport à l’origine du repère.


Utilisation des cookies
Lors de votre navigation sur ce site, des cookies nécessaires au bon fonctionnement et exemptés de consentement sont déposés.