CHAPITRE 8

Transformations dans le plan

NON COMMENCÉ

0 pts

Imprimer

1
NOTION D’HOMOTHÉTIE
2
PROPRIÉTÉS ET EFFETS D’UNE HOMOTHÉTIE

Notion d’homothétie

Définition

Homothétie

➔
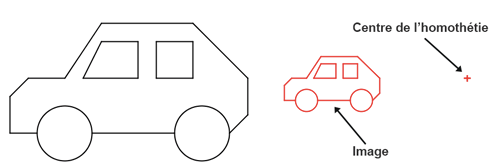
Une homothétie est une transformation qui agrandit ou rétrécit des figures à partir de la donnée d’un rapport et d’un centre.

Exemple

Avec une homothétie de rapport

0, 4

Remarque

Le rapport peut être positif :

Le point $B$ est l’image de $A$ par l'homothétie de centre $O$ et de rapport $k > 0$ si $B$ appartient à la demi-droite $[O A)$ et $O B = k \times O A$ .

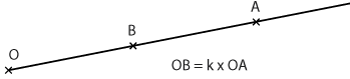Remarque

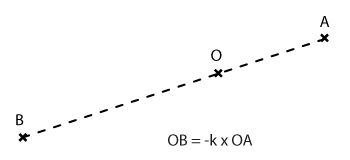
Le rapport peut être négatif :

Le point $B$ est l’image de $A$ par l’homothétie de centre $O$ et de rapport $k < 0$ si $A$ et $B$ sont de part et d'autre du point $O$ et $O B = - k \times O A$ .

Remarque

Lorsque le rapport est compris entre $- 1$ et $1$ , il s’agit d’une réduction, dans le cas contraire, c’est un agrandissement.
Lorsque deux triangles forment une configuration de Thalès, l'un est l'image de l'autre par une homothétie de centre le sommet commun.

Exemple

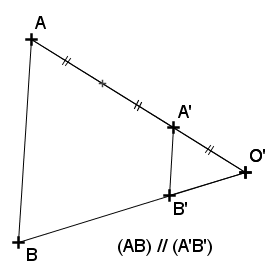
Le triangle

O^{'} A^{'} B^{'}

est une réduction du triangle

O^{'} A B

de rapport

\frac{1}{3}

, c’est l’image du triangle

O^{'} A B

par l’homothétie de centre

O^{'}

et de rapport

\frac{1}{3}

Exemple

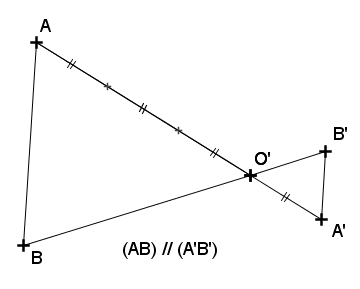
Pour cette nouvelle figure, le triangle

O^{'} A^{'} B^{'}

est une réduction du triangle

O^{'} A B

de rapport

\frac{- 1}{3}

, comme

A^{'}

n’est pas sur la demi-droite

[O^{'} A)

O^{'} A^{'} B^{'}

est l’image du triangle

O^{'} A B

par l’homothétie de centre

O^{'}

et de rapport

\frac{- 1}{3}

Afterclasse Premium

Objectifs du jour :0/3

Découvrir

Niveau 3ème >

Français Histoire Géographie Mathématiques SVT Physique-Chimie Espagnol Mentions légales

Mes enfants

Mes classes

Fermer

6ème 5ème 4ème 3ème 2nde Première Terminale

Mon Profil

remplacer

Mon Profil

remplacer

Mon Profil

remplacer

Transformations dans le plan

Notion d’homothétie

Définition

Homothétie

➔ Une homothétie est une transformation qui agrandit ou rétrécit des figures à partir de la donnée d’un rapport et d’un centre.

Exemple

Remarque

Remarque

Remarque

Exemple

Exemple

➔
Une homothétie est une transformation qui agrandit ou rétrécit des figures à partir de la donnée d’un rapport et d’un centre.