Inéquations

Définition

Inégalités strictes et larges

➔

Pour comparer des nombres, on utilise deux types de symboles :

• les symboles larges :
• $a\ge b$ : $a$ est supérieur ou égal à $b$ ;
• $a\le b$ : $a$ est inférieur ou égal à $b$.
• les symboles stricts :
• $a>b$ : $a$ est strictement supérieur à $b$ ;
• $a<b$ : $a$ est strictement inférieur à $b$.

Exemple

L’inégalité $1\le x<3$ est vérifiée pour tous les nombres allant de $1$ (inclus) à $3$ (exclus) et peut être représentée sur une droite graduée. Le sens des crochets à une signification : lorsque le crochet est ouvert vers l’extérieur de la ligne, la valeur n’est pas une solution : ici $3$ n’est pas une valeur possible de $x$ ; lorsque le crochet est ouvert vers l’intérieur de la ligne, la valeur est solution : ici $1$ est une valeur possible de $x$.

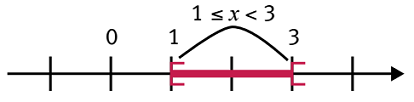Définition

Inéquation

➔

• On met deux expressions littérales en inéquation quand on veut savoir pour quelles valeurs des inconnues les membres de droite et de gauche vérifient une inégalité.
• On dit qu’un nombre est solution d’une inéquation quand l’inégalité est vérifiée lorsqu’on remplace une inconnue par ce nombre.
• Résoudre une inéquation, c’est trouver toutes ses solutions.