CHAPITRE 2

Calcul littéral et équations

0 pts

Imprimer

1
DÉVELOPPEMENT ET FACTORISATION
2
RÉSOLUTION D’UNE ÉQUATION

Identités remarquables

Rappel

Identités remarquables

➔
Ces égalités sont toujours vraies, pour tous nombres $a$ et $b$ :

$(a + b)^{2} = a^{2} + 2 a b + b^{2}$

$(a - b)^{2} = a^{2} - 2 a b + b^{2}$

$(a + b) (a - b) = a^{2} - b^{2}$

Exemple

Consigne :
Factorisez l’expression

A = x^{2} + 2 x + 1

.

Correction :

A = x^{2} + 2 x + 1

est de la forme

a^{2} + 2 a b + b^{2}

avec

a = x

b = 1

A = (x)^{2} + (2 \times 1 \times x) + (1)^{2}

A = (x + 1)^{2}

Développement double

Rappel

Développement double

➔
On a toujours :

$(a + b) (c + d) = a \times c + a \times d + b \times c + b \times d$

Exemple

Consigne :
Développez l'expression

(2 + x) (x + 3)

.

Correction :

(2 + x) (x + 3) = 2 \times x + 2 \times 3 + x \times x + x \times 3

(2 + x) (x + 3) = 2 x + 6 + x^{2} + 3 x

(2 + x) (x + 3) = x^{2} + 5 x + 6

Développement et factorisation

Rappel

Développement

➔
Développer une expression, c’est transformer un produit en somme grâce à la propriété de distributivité.

Exemple

Consigne :
Développez l’expression

3 (5 + x)

.

Correction :

3 (5 + x) = 3 \times (5 + x)

3 (5 + x) = 3 \times 5 + 3 \times x

3 (5 + x) = 15 + 3 x

Rappel

Factorisation

➔
Factoriser une expression, c’est transformer une somme en produit grâce à la propriété de distributivité.

Exemple

Consigne :
Factorisez l’expression

8 z + 5 z

.

Correction :

8 z + 5 z = z \times 8 + z \times 5

8 z + 5 z = z \times (8 + 5)

8 z + 5 z = z \times 13

8 z + 5 z = 13 z

Remarque

Développer ou factoriser permet de réduire une expression. C’est-à-dire, faire en sorte qu’elle comporte le moins de symboles et nombres possibles.

Distributivité

Rappel

Distributivité

➔
Pour tout nombre $k$ , $m$ et $n$ . On a toujours :

$k \times (m + n) = k \times m + k \times n$

Remarque

La propriété de distributivité permet de transformer une somme en produit, ou un produit en somme.

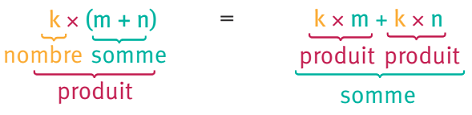Démontrez une propriété par le calcul littéral

Rappel

Utilisation

➔
On peut montrer que deux expressions littérales sont égales à l'aide du calcul littéral.

Exemple

Consigne :
Montrez que pour tous nombres

a, b, c

avec

c \neq = 0

\frac{a}{c} + \frac{b}{c} = \frac{a + b}{c}

Correction :
À l'aide de la propriété de distributivé, nous obtenons :

(\frac{a}{c} + \frac{b}{c}) \times c = \frac{a}{c} \times c + \frac{b}{c} \times c

(\frac{a}{c} + \frac{b}{c}) \times c = a + b

donc

(\frac{a}{c} + \frac{b}{c}) \times \frac{c}{c} = \frac{a + b}{c}

On a donc bien

\frac{a}{c} + \frac{b}{c} = \frac{a + b}{c}

Niveau 3ème >

Français Histoire Géographie Mathématiques SVT Physique-Chimie Espagnol Mentions légales

Mes enfants

Fermer

6ème 5ème 4ème 3ème 2nde Première Terminale

Mon Profil

remplacer

Mon Profil

remplacer

Mon Profil

remplacer

Utilisation des cookies

Lors de votre navigation sur ce site, des cookies nécessaires au bon fonctionnement et exemptés de consentement sont déposés.

Calcul littéral et équations

Identités remarquables

Rappel

Identités remarquables

➔ Ces égalités sont toujours vraies, pour tous nombres a et b : (a+b)2=a2+2ab+b2 (a−b)2=a2−2ab+b2 (a+b)(a−b)=a2−b2

Exemple

Développement double

Rappel

Développement double

➔ On a toujours : (a+b)(c+d)=a×c+a×d+b×c+b×d

Exemple

Développement et factorisation

Rappel

Développement

➔ Développer une expression, c’est transformer un produit en somme grâce à la propriété de distributivité.

Exemple

Rappel

Factorisation

➔ Factoriser une expression, c’est transformer une somme en produit grâce à la propriété de distributivité.

Exemple

Remarque

Distributivité

Rappel

Distributivité

➔ Pour tout nombre k, m et n. On a toujours : k×(m+n)=k×m+k×n

Remarque

Démontrez une propriété par le calcul littéral

Rappel

Utilisation

➔ On peut montrer que deux expressions littérales sont égales à l'aide du calcul littéral.

Exemple

➔
Ces égalités sont toujours vraies, pour tous nombres $a$ et $b$ :

$(a + b)^{2} = a^{2} + 2 a b + b^{2}$

$(a - b)^{2} = a^{2} - 2 a b + b^{2}$

$(a + b) (a - b) = a^{2} - b^{2}$

➔
On a toujours :

$(a + b) (c + d) = a \times c + a \times d + b \times c + b \times d$

➔
Développer une expression, c’est transformer un produit en somme grâce à la propriété de distributivité.

➔
Factoriser une expression, c’est transformer une somme en produit grâce à la propriété de distributivité.

➔
Pour tout nombre $k$ , $m$ et $n$ . On a toujours :

$k \times (m + n) = k \times m + k \times n$

➔
On peut montrer que deux expressions littérales sont égales à l'aide du calcul littéral.