CHAPITRE 5

Puissances

NON COMMENCÉ

0 pts

Imprimer

1
NOTION DE PUISSANCE
2
CALCULS AVEC LES PUISSANCES
3
ÉCRITURE SCIENTIFIQUE

Signe d’une puissance

Propriété

Signe d’une puissance

➔
Si $a$ est un nombre non nul et $n$ un entier non nul :

si $a > 0$ , alors $a^{n} > 0$ ;

si $a < 0$ :

si $n$ est pair, alors $a^{n} > 0$

si $n$ est impair, alors $a^{n} < 0$

Exemple

$2^{4} > 0$
$(- 2)^{3} = - 8 < 0$
$3^{- 3} = \frac{1}{2 7} > 0$
$(- 2)^{2} = 4 > 0$
$(- 2)^{- 3} = - \frac{1}{8} < 0$

Puissance à exposant négatif

Définition

Puissance à exposant négatif

➔
Pour tout nombre $a$ non nul et tout entier positif $n$ , une puissance de $a$ à l’exposant négatif $- n$ s’écrit :

$a^{- n} = \frac{1}{a ^{n}}$

Exemple

$\frac{1}{5 ^{4}} = 5^{- 4}$
$7^{3} = \frac{1}{7 ^{- 3}}$

Remarque

a^{- n}

est l’inverse de

a^{n}

Puissance à exposant positif

Définition

Puissance à exposant positif

➔

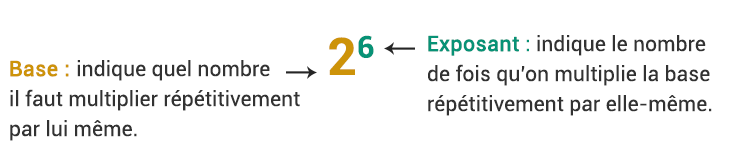
Les puissances sont une abréviation d’écriture pour les produits composés d’un même facteur répété plusieurs fois.

Au lieu d’écrire $2 \times 2 \times 2 \times 2 \times 2 \times 2$ , on peut écrire $2^{6}$ et on lit « 2 puissance 6 ».

Remarque

La base d’une puissance peut également être un nombre négatif.
On se sert de parenthèses pour indiquer que le signe «

-

» fait partie de la base.

Exemple

(- 3)^{2} = (- 3) \times (- 3) = 9

alors que

- 3^{2} = - (3 \times 3) = - 9

Remarque

Quelle que soit la valeur de

a

a^{0} = 1

Afterclasse Premium

Objectifs du jour :0/3

Découvrir

Niveau 3ème >

Français Histoire Géographie Mathématiques SVT Physique-Chimie Espagnol Mentions légales

Mes enfants

Mes classes

Fermer

6ème 5ème 4ème 3ème 2nde Première Terminale

Mon Profil

remplacer

Mon Profil

remplacer

Mon Profil

remplacer

Utilisation des cookies

Lors de votre navigation sur ce site, des cookies nécessaires au bon fonctionnement et exemptés de consentement sont déposés.

Puissances

Signe d’une puissance

Propriété

Signe d’une puissance

➔ Si a est un nombre non nul et n un entier non nul : si a>0, alors an>0 ; si a<0 : si n est pair, alors an>0 si n est impair, alors an<0

Exemple

Puissance à exposant négatif

Définition

Puissance à exposant négatif

➔ Pour tout nombre a non nul et tout entier positif n, une puissance de a à l’exposant négatif −n s’écrit : a−n=an1​

Exemple

Remarque

Puissance à exposant positif

Définition

Puissance à exposant positif

➔ Les puissances sont une abréviation d’écriture pour les produits composés d’un même facteur répété plusieurs fois. Au lieu d’écrire 2×2×2×2×2×2, on peut écrire 26 et on lit « 2 puissance 6 ».

Remarque

Exemple

Remarque

➔
Si $a$ est un nombre non nul et $n$ un entier non nul :

si $a > 0$ , alors $a^{n} > 0$ ;

si $a < 0$ :

si $n$ est pair, alors $a^{n} > 0$

si $n$ est impair, alors $a^{n} < 0$

➔
Pour tout nombre $a$ non nul et tout entier positif $n$ , une puissance de $a$ à l’exposant négatif $- n$ s’écrit :

$a^{- n} = \frac{1}{a ^{n}}$

➔

Les puissances sont une abréviation d’écriture pour les produits composés d’un même facteur répété plusieurs fois.

Au lieu d’écrire $2 \times 2 \times 2 \times 2 \times 2 \times 2$ , on peut écrire $2^{6}$ et on lit « 2 puissance 6 ».