CHAPITRE 10

Triangles

0 pts

Imprimer

1
PROPRIÉTÉS SUR LES TRIANGLES
2
DROITES REMARQUABLES D’UN TRIANGLE

Les angles d’un triangle

Rappel

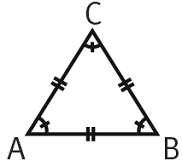
Triangle équilatéral

➔
Un triangle équilatéral $A B C$ a trois angles de même mesure :

$A B C = B A C = A C B$

Rappel

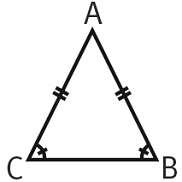
Triangle isocèle

➔
Un triangle isocèle en $A$ a deux angles de même mesure :

$A B C = A C B$

Propriété

Somme d’un triangle

➔
La somme des angles d’un triangle est égale à $18 0^{\circ}$ .

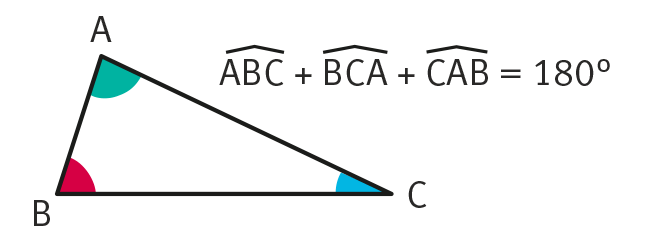
Exemple

Consigne :

A B C

est un triangle. On connait les mesures de deux de ses angles :

A C B = 8 0^{\circ}

A B C = 6 0^{\circ}

.
Combien mesure le troisième angle ?

Correction :

180 - 80 - 60 = 40

L’angle

B A C

mesure

4 0^{\circ}

Les inégalités triangulaires

Propriété

Triangle

➔
Dans un triangle $A B C$ , la longueur d’un côté est toujours plus petite que la somme des longueurs des deux autres côtés :

$A B \leq A C + B C$

$A C \leq A B + B C$

$B C \leq A B + A C$

Remarque

Si dans un triangle

A B C

, l’égalité

A B = A C + B C

est vérifiée, alors

C

appartient au segment

[A B]

. Le triangle est plat.

Exemple

Consigne :
Voici des mesures de segments :

$A B = 3 c m; A C = 4 c m; B C = 5 c m$ .
$A B = 8 c m; A C = 3, 7 c m; B C = 3, 9 c m$ .
$A B = 5 c m; A C = 2, 2 c m; B C = 3 c m$ .

Lesquels peuvent servir à construire un triangle ?

Correction :
Les triplés des segments

1

3

peuvent servir à construire un triangle.
Dans le triplé de segments

2

, un des segments est plus long que la somme des deux autres. Ce triplé ne peut donc pas servir à construire un triangle.

Niveau 3ème >

Français Histoire Géographie Mathématiques SVT Physique-Chimie Espagnol Mentions légales

Mes enfants

Fermer

6ème 5ème 4ème 3ème 2nde Première Terminale

Mon Profil

remplacer

Mon Profil

remplacer

Mon Profil

remplacer

Utilisation des cookies

Lors de votre navigation sur ce site, des cookies nécessaires au bon fonctionnement et exemptés de consentement sont déposés.

Triangles

Les angles d’un triangle

Rappel

Triangle équilatéral

➔ Un triangle équilatéral ABC a trois angles de même mesure : ABC=BAC=ACB

Rappel

Triangle isocèle

➔ Un triangle isocèle en A a deux angles de même mesure : ABC=ACB

Propriété

Somme d’un triangle

➔ La somme des angles d’un triangle est égale à 180∘.

Exemple

Les inégalités triangulaires

Propriété

Triangle

➔ Dans un triangle ABC, la longueur d’un côté est toujours plus petite que la somme des longueurs des deux autres côtés : AB≤AC+BC AC≤AB+BC BC≤AB+AC

Remarque

Exemple

➔
Un triangle équilatéral $A B C$ a trois angles de même mesure :

$A B C = B A C = A C B$

➔
Un triangle isocèle en $A$ a deux angles de même mesure :

$A B C = A C B$

➔
La somme des angles d’un triangle est égale à $18 0^{\circ}$ .

➔
Dans un triangle $A B C$ , la longueur d’un côté est toujours plus petite que la somme des longueurs des deux autres côtés :

$A B \leq A C + B C$

$A C \leq A B + B C$

$B C \leq A B + A C$