CHAPITRE 2
Nombres relatifs
- NOMBRES RELATIFS ET REPÉRAGE1
- ADDITION ET SOUSTRACTION2
Comparer des nombres relatifs
Définition
Définition
Comparer deux nombres
➔ Comparer deux nombres, c’est dire si l’un est strictement inférieur ou supérieur à l’autre, ou s’ils sont égaux.
➔
Propriété
Propriété
Règles de comparaison
➔
- Si les deux nombres sont de signes opposés :
- le nombre négatif est alors strictement inférieur au nombre positif, sauf si les deux nombres sont nuls.
- Si les deux nombres sont de même signe :
- s’ils sont positifs, le plus petit est celui qui est le plus proche de 0, donc dont la distance à zéro est la plus petite.
- s’ils sont négatifs, le plus petit est celui qui est le plus éloigné de 0, donc dont la distance à zéro est la plus grande.
- Dans tous les cas, le nombre le plus petit est celui qui est situé le plus à gauche sur une droite graduée.
➔
- le nombre négatif est alors strictement inférieur au nombre positif, sauf si les deux nombres sont nuls.
- s’ils sont positifs, le plus petit est celui qui est le plus proche de 0, donc dont la distance à zéro est la plus petite.
- s’ils sont négatifs, le plus petit est celui qui est le plus éloigné de 0, donc dont la distance à zéro est la plus grande.
Exemple
Exemple
Pour comparer ces nombres, on lit de gauche à droite sur la droite orientée.
On a donc −2,5<−1<0<1<3,2.  |
Se repérer avec les nombres relatifs
Règle
Règle
Repérage sur une droite graduée
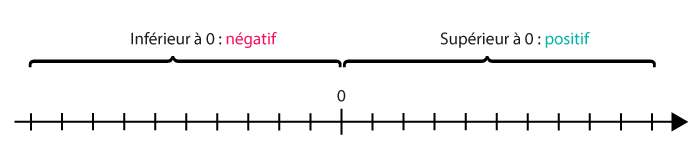
➔ Sur une droite graduée orientée, on représente les nombres positifs à droite de zéro et les nombres négatifs à gauche de zéro.
➔
Règle
Règle
Construire un repère orthogonal
➔
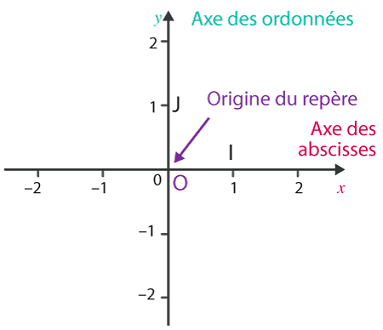
- On trace deux axes perpendiculaires :
- un axe (Ox), souvent horizontal, orienté vers la droite. C’est l’axe des abscisses ;
- un axe (Oy), souvent vertical, orienté vers le haut. C’est l’axe des ordonnées ;
- l’intersection de ces deux axes est l’origine du repère, qu’on appelle généralement O.
- On définit une unité. On place un point I sur l’axe des abscisses et un point J sur l’axe des ordonnées afin de définir l’unité de longueur OI=OJ=1. Ce repère est noté le repère (O,I,J).
➔
- un axe (Ox), souvent horizontal, orienté vers la droite. C’est l’axe des abscisses ;
- un axe (Oy), souvent vertical, orienté vers le haut. C’est l’axe des ordonnées ;
- l’intersection de ces deux axes est l’origine du repère, qu’on appelle généralement O.
Règle
Règle
Placer un repère
➔
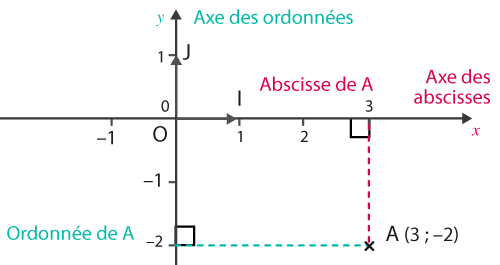
- Pour placer un point dans un repère, on utilise 2 nombres : l’abscisse et l’ordonnée.
- Si un point A a pour abscisse le nombre a et pour ordonnée le nombre b, on le note A(a ; b).
➔
Exemple
Exemple
Sur le repère précédent, le point A(3 ; −2) a pour abscisse 3 et pour ordonnée −2.
|
Définitions
Définition
Définition
Nombres relatifs
➔
- On écrit un nombre relatif avec un signe (+ : signe positif ; − : signe négatif) et un nombre appelé « distance à zéro ».
- Un nombre positif est un nombre supérieur à 0.
- ex. : 2,7 ; 4 150 ; 0,8.
- Un nombre négatif est un nombre inférieur à 0.
- ex. : −5 ; −1431 ; −0,4.
- Les nombres positifs et négatifs forment l’ensemble des nombres relatifs.
➔
- ex. : 2,7 ; 4 150 ; 0,8.
- ex. : −5 ; −1431 ; −0,4.

Remarque
Remarque
Le nombre zéro est à la fois de signe positif et négatif.
|
Exemple
Exemple
|
Définition
Définition
Opposé d’un nombre
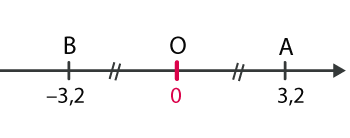
➔ L’opposé d’un nombre est le nombre de signe contraire qui est à la même distance de zéro.
➔
Exemple
Exemple
 |
Remarque
Remarque
|
Utilisation des cookies
Lors de votre navigation sur ce site, des cookies nécessaires au bon fonctionnement et exemptés de consentement sont déposés.