CHAPITRE 11
Triangles, rectangles et losanges
- PROPRIÉTÉS DES TRIANGLES USUELS1
- PROPRIÉTÉS DES QUADRILATÈRES USUELS2
- À SAVOIR REFAIRE
Triangle équilatéral
Définition
Définition
Triangle équilatéral
➔ Un triangle équilatéral est un triangle qui possède trois côtés de même longueur : il est isocèle en chacun de ses sommets.
➔
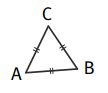
Propriété
Propriété
Axes de symétrie
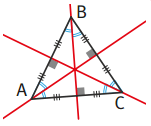
➔ Un triangle équilatéral possède toujours trois axes de symétrie : ce sont les médiatrices de chaque côté. Ces médiatrices sont aussi les bissectrices de chaque angle.
- Dans ce triangle équilatéral ABC, les trois droites rouges sont les axes de symétrie du triangle.
➔
Propriété
Propriété
Angles d’un triangle équilatéral
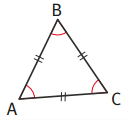
➔ Les trois angles d’un triangle équilatéral ABC sont égaux.
- ABC=CAB=BCA
➔
Triangle isocèle
Définition
Définition
Triangle isocèle
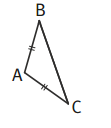
➔ Un triangle isocèle est un triangle qui possède deux côtés de longueurs égales.
- On dit que le triangle ABC est isocèle en A. Cela veut dire que AB=AC !
➔
Propriété
Propriété
Bissectrice et médiatrice du triangle isocèle
➔
- Si ABC est un triangle isocèle en A, alors la bissectrice de CAB est aussi la médiatrice de [BC].
- Un triangle ABC isocèle en A possède un axe de symétrie : c’est la médiatrice de [BC].
➔
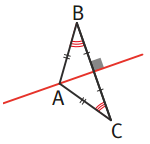
Remarque
Remarque
Un triangle isocèle posséde parfois plus d’un axe de symétrie, dans ce cas, c’est un triangle équilatéral.
|
Propriété
Propriété
Triangle isocèle
➔
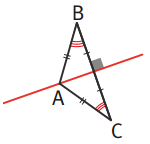
- Un triangle isocèle possède deux côtés égaux et deux angles égaux.
- Si un triangle possède deux angles égaux, alors il est isocèle !
- Dans la symétrie par rapport à la droite rouge, A est le symétrique de A et C est le symétrique de B.
- Donc l’angle BCA est le symétrique de l’angle ABC.
- On sait que la symétrie conserve les angles.
- On a donc par symétrie : ABC=BCA
➔
- Donc l’angle BCA est le symétrique de l’angle ABC.
- On sait que la symétrie conserve les angles.
- On a donc par symétrie : ABC=BCA
Triangle rectangle
Définition
Définition
Triangle rectangle
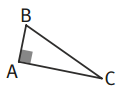
➔ Un triangle rectangle est un triangle possédant un angle droit.
- On dit que le triangle ABC est rectangle en A. Cela permet de savoir où est l’angle droit !
➔
Remarque
Remarque
Il ne peut y avoir qu’un seul angle droit dans un triangle.
|
Utilisation des cookies
Lors de votre navigation sur ce site, des cookies nécessaires au bon fonctionnement et exemptés de consentement sont déposés.