CHAPITRE 5

Fractions

0 pts

1
PRÉSENTATION DES FRACTIONS
2
PROPRIÉTÉS DES FRACTIONS
3
UTILISER LES FRACTIONS
À SAVOIR REFAIRE

Placer une fraction sur un axe gradué

Règle

Placer une fraction sur un axe

➔
Il existe plusieurs méthodes pour placer une fraction sur un axe. Par exemple, pour placer $\frac{4}{7}$ :

soit diviser $4$ unités en $7$ .

Soit diviser $1$ unité en $7$ et la reporter $4$ fois au compas.

Pour diviser une unité, on peut utiliser au choix :

le quadrillage.

Un « guide-âne ».

Une règle graduée.

Définition

Remarque

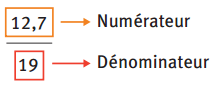
Une fraction peut être vue de trois manières différentes :

comme une proportion ;
comme un nombre ;
comme un quotient.

Exemple

La fraction $\frac{9}{7}$ : on a divisé une quantité en $7$ portions.
Chaque portion représente $\frac{1}{7}$ .
$9$ portions représentent $9 \times \frac{1}{7} = \frac{9}{7}$ .

Exemple

La fraction $\frac{9}{7}$ est un nombre dont une valeur approchée au centième est $1, 29$ : $\frac{9}{7} \approx 1, 29$ .

Exemple

La fraction $\frac{9}{7}$ est le quotient de $9$ par $7$ : $7 \times \frac{9}{7} = 9$ .

Remarque

Écrire une fraction, c’est juste écrire différemment un quotient.

Rappel

➔

Le quotient de $a$ par $b$ $(a \div b)$ est le nombre qui, multiplié par $b$ , donne $a$ .

Ainsi $\frac{a}{b} = a \div b$ et $b \times \frac{a}{b} = a$ .

Remarque

Tout nombre décimal peut s’écrire sous forme de fraction, c’est l’écriture fractionnaire.

Exemple

2, 57 = \frac{2 5 7}{1 0 0}

Remarque

Toute fraction n’est pas un nombre décimal. Par exemple

\frac{1}{7}

ne peut s’écrire autrement que

\frac{1}{7}

Si on en veut une valeur exacte, on est obligé d’en garder une écriture fractionnaire.
Par contre, si on en veut une valeur approchée, on peut écrire $\frac{1}{7} \approx 0, 143$ . (Attention : ce n’est pas une égalité !)
$\frac{1}{2}$ s’écrit $\frac{1}{2}$ ou $0, 5$ indifféremment.

Exemple

\frac{1}{3}

ne peut s’écrire avec un nombre fini de chiffres après la virgule, la division donne

0, 3333

…
Ce n’est donc pas un nombre décimal !

Remarque

b \neq = 0

on a toujours

\frac{b}{b} = 1

car

b \times 1 = b

.
Ex. :

\frac{7}{7} = 1

Niveau 3ème >

Français Histoire Géographie Mathématiques SVT Physique-Chimie Espagnol Mentions légales

Mes enfants

Fermer

6ème 5ème 4ème 3ème 2nde Première Terminale

Mon Profil

remplacer

Mon Profil

remplacer

Mon Profil

remplacer

Utilisation des cookies

Lors de votre navigation sur ce site, des cookies nécessaires au bon fonctionnement et exemptés de consentement sont déposés.

Fractions

Placer une fraction sur un axe gradué

Règle

Placer une fraction sur un axe

Définition

Remarque

Exemple

Exemple

Exemple

Remarque

Rappel

➔ Le quotient de a par b (a÷b) est le nombre qui, multiplié par b, donne a. Ainsi ba​=a÷b et b×ba​=a.

Remarque

Exemple

Remarque

Exemple

Remarque

➔

Le quotient de $a$ par $b$ $(a \div b)$ est le nombre qui, multiplié par $b$ , donne $a$ .

Ainsi $\frac{a}{b} = a \div b$ et $b \times \frac{a}{b} = a$ .