CHAPITRE 4
Multiplication, division décimale
- MAÎTRISER LES OPÉRATIONS ET LEURS PROPRIÉTÉS1
- MULTIPLIER UN NOMBRE DÉCIMAL PAR 0,1; 0,01; 0,001, ETC.2
- CALCULER L’ORDRE DE GRANDEUR D’UNE MULTIPLICATION3
- À SAVOIR REFAIRE
La division décimale
Remarque
Remarque
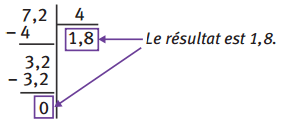
Lorsque l’on effectue la division décimale, le calcul devrait se poursuivre jusqu’au bout, c’est-à-dire quand le reste s’annule.
|
Exemple
Exemple
 |
Remarque
Remarque
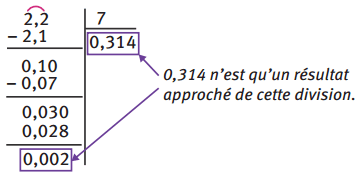
On ne peut pas toujours poursuivre le calcul d’une division décimale jusqu’au bout : il peut se prolonger indéfiniment. Dans ce cas, on ne peut pas calculer son résultat exact.
|
Exemple
Exemple
 |
Définition
Définition
Quotient
➔ Le quotient est le résultat de la division d’un dividende par un diviseur.
➔

Remarque
Remarque
Le quotient 7,2÷4 est le nombre x vérifiant 4×x=7,2.
Ainsi :
7,4×x=25,16 que vaut x ?
|
Exemple
Exemple
|
Remarque
Remarque
|
Remarque
Remarque
Le quotient de deux nombres n’est pas nécessairement un nombre décimal.
|
Exemple
Exemple
1÷3=0,3333... Quel est le quotient ?
La division ne s’arrête jamais, le quotient 1÷3 n’a pas d’écriture décimale. Il faut utiliser le mot « environ ». |
Rappel
Rappel
Vocabulaire de la division :
➔
- Moitié : division par 2, ou multiplication par 0,5.
- Tiers : division par 3.
- Quart : division par 4, ou multiplication par 0,25.
➔
La multiplication
Définition
Définition
Multiplication
➔ La multiplication de deux facteurs s’appelle le produit.
➔
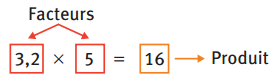
Propriété
Propriété
L'ordre dans une multiplication
➔ Le produit ne dépend pas de l’ordre dans lequel on a multiplié les facteurs.
- a×b=b×a
- 4×5=5×4
➔
Propriété
Propriété
Regrouper les nombres dans une multiplication
➔ Le produit ne dépend pas de la façon dont on a regroupé les facteurs.
- 2×3×4=6×4=24
- 2×3×4=2×12=24
➔
Remarque
Remarque
|
Remarque
Remarque
|
Rappel
Rappel
Vocabulaire de la multiplication :
➔
- Double : multiplication par 2.
- Triple : multiplication par 3.
- Quadruple : multiplication par 4.
➔
Utilisation des cookies
Lors de votre navigation sur ce site, des cookies nécessaires au bon fonctionnement et exemptés de consentement sont déposés.