CHAPITRE 2
Les nombres décimaux
- LES DIFFÉRENTES FACETTES DES NOMBRES DÉCIMAUX1
- COMPARER DES NOMBRES DÉCIMAUX2
- VALEURS APPROCHÉES3
- À SAVOIR REFAIRE
Multiplier et diviser un nombre décimal par 10 ; 100 ; 1 000, etc.
Règle
Règle
Multiplier un nombre décimal
➔
- Multiplier un nombre par 10 revient à décaler le nombre d’un cran vers la gauche.
- 2,38678×10=23,8678
- Quand il n’y a pas assez de chiffres à droite, on rajoute des zéros « inutiles ».
- 15×10=15,0×10=150
- Multiplier un nombre par 100 revient à décaler le nombre de deux crans vers la gauche.
- 74,398×100=7439,8 et 48,3×100=48,30×100=4 830
- Multiplier un nombre par 1 000 revient à décaler le nombre de trois crans vers la gauche.
- 21,369×1 000=21369 et 24,5×1 000=24,500×1 000=24 500
➔
- 2,38678×10=23,8678
- 15×10=15,0×10=150
- 74,398×100=7439,8 et 48,3×100=48,30×100=4 830
- 21,369×1 000=21369 et 24,5×1 000=24,500×1 000=24 500
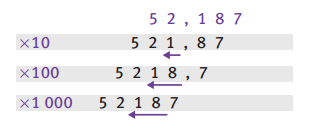
Règle
Règle
Diviser un nombre décimal
➔
- Diviser un nombre par 10 revient à décaler le nombre d’un cran vers la droite.
- 1 635,7÷10=163,57
- Lorsqu’il n’y a pas assez de chiffres à gauche, on rajoute un zéro « inutile ».
- 3,4÷10=03,4÷10=0,34
- Diviser un nombre par 100 revient à décaler le nombre de deux crans vers la droite.
- 981,35÷100=9,8135 et 17,35÷100=0,1735
- Diviser un nombre par 1 000 revient à décaler le nombre de trois crans vers la droite
- 4 172÷1 000=4 172,0÷1 000=4,172
➔
- 1 635,7÷10=163,57
- 3,4÷10=03,4÷10=0,34
- 981,35÷100=9,8135 et 17,35÷100=0,1735
- 4 172÷1 000=4 172,0÷1 000=4,172

Écrire les nombres décimaux
Définition
Définition
Nombre décimal
➔ Un nombre décimal est le quotient (ou la fraction) d’un nombre entier sur 10, 100, 1000, etc.
➔
Exemple
Exemple
|
Définition
Définition
Fraction décimale
➔ La fraction décimale d’un nombre décimal est son écriture sous forme de fraction d’un entier « sur » 10 ; 100 ou 1000, etc.
➔
Exemple
Exemple
|
Définition
Définition
Écriture décimale
➔
- L’écriture décimale d’un nombre décimal est son écriture sous forme de nombre à virgule.
- Un nombre décimal s’écrit toujours avec un nombre fini de chiffres après la virgule.
➔
Exemple
Exemple
|
Remarque
Remarque
Certains zéros peuvent ne pas être utiles dans une écriture décimale. Ils sont situés soit à gauche de la virgule soit en fin de nombre.
|
Exemple
Exemple
|
Utilisation des cookies
Lors de votre navigation sur ce site, des cookies nécessaires au bon fonctionnement et exemptés de consentement sont déposés.