1

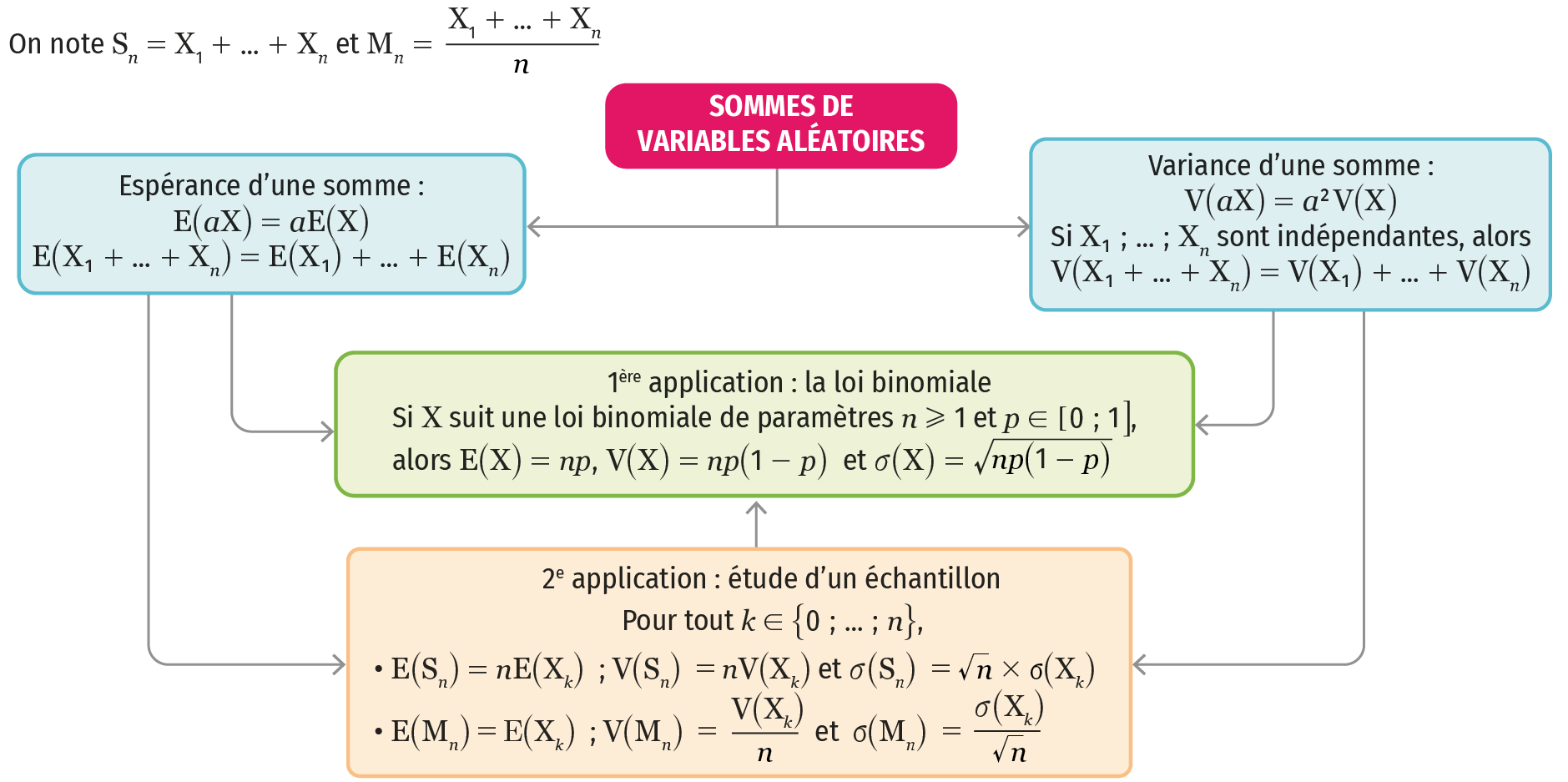
Si $\text{X}$ et $\text{Y}$ sont deux variables aléatoires définies sur un univers $\Omega$ et si $\mathbf{a}$ est un nombre réel, on a les égalités $\mathbf{E}(\mathbf{X}+\mathbf{Y})=\mathbf{E}(\mathbf{X})+\mathbf{E}(\mathbf{Y}),\mathbf{E}(\mathbf{a}\mathbf{X})=\mathbf{a}\mathbf{E}(\mathbf{X})\mathrm{et}\mathbf{E}(\mathbf{a}\mathbf{X}+\mathbf{Y})=\mathbf{a}\mathbf{E}(\mathbf{X})+\mathbf{E}(\mathbf{Y})$. Cela permet de :

✔ déterminer l’espérance d’une variable aléatoire en la décomposant comme somme de variables aléatoires plus simples à étudier ;
✔ démontrer que si $\text{X}$ suit la loi binomiale de paramètres $n$ et $p$, alors $\mathrm{E}(\mathrm{X})=np$.

2

Si $\text{X}$ et $\text{Y}$ sont deux variables aléatoires indépendantes définies sur un univers $\Omega$ et si $\mathbf{a}$ est un nombre réel, on a les égalités $\mathbf{V}(\mathbf{X}+\mathbf{Y})=\mathbf{V}(\mathbf{X})+\mathbf{V}(\mathbf{Y})\text{ et }\mathbf{V}(\mathbf{a}\mathbf{X})={\mathbf{a}}^2\mathbf{V}(\mathbf{X})$.  :

✔ déterminer la variance d’une variable aléatoire en la décomposant comme somme de variables aléatoires indépendantes plus simples à étudier ;
✔ démontrer que si $\text{X}$ suit la loi binomiale de paramètres $n$ et $p$, alors $\mathrm{V}(\mathrm{X})=np(1-p)$ et $\sigma (\mathrm{X})=\sqrt{np(1-p)}$.

3

Étude de la somme ${\mathbf{S}}_n$ de $n$ variables aléatoires indépendantes ${\mathbf{X}}_1;\dots ;{\mathbf{X}}_n$ suivant la même loi de probabilité. La variable aléatoire ${\mathbf{S}}_n$ s’écrit ${\mathbf{S}}_n={\mathbf{X}}_1+\dots +{\mathbf{X}}_n$. Cela permet de :

✔ étudier plus simplement les propriétés de la somme, notamment dans le cas de la répétition de $n$ expériences dans des conditions indépendantes ;
✔ calculer l’espérance de ${\mathrm{S}}_n$ en utilisant, pour tout $k\in \{1;\dots ;n\},\mathrm{E}\left({\mathrm{S}}_n\right)=n\mathrm{E}\left({\mathrm{X}}_k\right)$ ;
✔ calculer l’espérance de ${\mathrm{S}}_n$ en utilisant $\mathrm{V}\left({\mathrm{S}}_n\right)=n\mathrm{V}\left({\mathrm{X}}_k\right)$. On a ainsi $\sigma \left({\mathrm{S}}_n\right)=\sqrt{n}\sigma \left({\mathrm{X}}_k\right)$.

4

Étude de la moyenne ${\mathbf{M}}_n$ de n variables aléatoires indépendantes ${\mathbf{X}}_1;\dots ;{\mathbf{X}}_n$ suivant la même loi de probabilité. La variable aléatoire ${\mathbf{M}}_n$ s’écrit ${\mathbf{M}}_n=\frac{{\mathbf{X}}_1+\dots +{\mathbf{X}}_n}{\mathbf{n}}$. Cela permet de :

✔ étudier plus simplement les propriétés de la moyenne, notamment dans le cas de la répétition de $n$ expériences dans des conditions indépendantes ;
✔ calculer l’espérance de ${\mathbf{M}}_n$ en utilisant, pour tout $k\in \{1;\dots ;n\},\mathrm{E}\left({\mathrm{M}}_n\right)=\mathrm{E}\left({\mathrm{X}}_k\right)$ ;
✔ calculer l’espérance de ${\mathbf{M}}_n$ en utilisant $V\left(M_n\right)=\frac{V\left(X_k\right)}{n}$. On a ainsi $\sigma \left({\mathrm{M}}_n\right)=\frac{\sigma \left({\mathrm{X}}_k\right)}{\sqrt{n}}$.