undefined - Fiche de révision Afterclasse

CHAPITRE

0 pts

Rappels sur le théorème de Pythagore

Cosinus, sinus et tangente d’un angle

Formules de trigonométrie

Formules et Théorèmes

À savoir refaire

Cosinus, sinus et tangente d’un angle

- ARappel sur les angles aigu et obtus
  - Définition
    Angles aigus et obtus
    
    Un angle aigu est un angle inférieur à $90^\circ$ .
    
    Un angle obtus est un angle compris entre $90^\circ$ et $180^\circ$ .
- BCosinus, sinus et tangente d’un angle aigu
  - Formule
    Cosinus
    Dans un triangle rectangle, on définit le cosinus d’un angle aigu $\alpha$ comme :
    
    $\text{cosinus} \; \alpha=\frac{\text{c}{\hat{\text{o}}\text{t} \acute{\text{e}}\text{ adjacent }\grave{\text{a}} \ \alpha }}{\text{hypot}\acute{\text{e}}\text{nuse}}$
    
    On note $\cos(\alpha)$ .
    
    Le cosinus d'un angle aigu est toujours compris entre $0$ et $1$ .
  - Formule
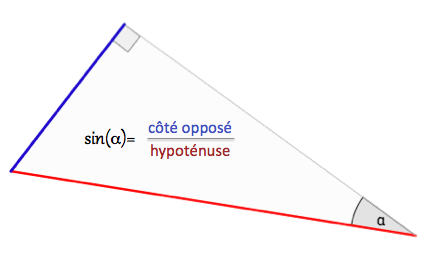
    Sinus
    Dans un triangle rectangle, on définit le sinus d’un angle aigu $\alpha$ comme :
    
    $\text{sinus} \; \alpha=\frac{\text{c}{\hat{\text{o}}}\text{t} \acute{\text{e}}\text{ oppos}\acute{\text{e}} \ \grave{\text{a}} \ \alpha }{\text{hypot}\acute{\text{e}}\text{nuse}}$ .
    
    On note $\sin(\alpha)$ .
    
    Le sinus d'un angle aigu est toujours compris entre 0 et 1.
  - Formule
    Tangente
    Dans un triangle rectangle, on définit la tangente d’un angle aigu $\alpha$ comme :
    
    $\text{tangente} \; \alpha=\frac{\text{c}{\hat{\text{o}}}\text{t} \acute{\text{e}}\text{ oppos}\acute{\text{e}} \ \grave{\text{a}} \ \alpha }{\text{c}{\hat{\text{o}}\text{t} \acute{\text{e}}\text{ adjacent }\grave{\text{a}} \ \alpha }}$ .
    
    On note $\tan(\alpha)$ .
    
    À l'inverse du sinus et du cosinus, la tangente peut être supérieure à $1$ .
  - Exemple
    $\cos(\hat{ACB}) = \cos(53,13^\circ) = 0,6$ (calculatrice) et $\frac{BC}{AC} = \frac{3}{5} = 0,6$
    
    $\sin(\hat{ACB}) = \sin(53,13^\circ) = 0,8$ (calculatrice) et $\frac{AB}{AC} = \frac{4}{5} = 0,8$
    
    $\tan(\hat{ACB}) = \tan(53,13^\circ) = 1,33$ (calculatrice) et $\frac{AB}{BC} = \frac{4}{3} = 1,33$
    
    Attention ! Les valeurs données ici sont approchées.
  - Remarque
    Tu retiendras plus facilement ces formules grâce au moyen mnémotechnique : SOH-CAH-TOA.
    
    SOH : $\text{Sinus}=\frac{\text{ Oppos}\acute{\text{e}}}{\text{Hypot}\acute{\text{e}}\text{nuse}}$
    
    CAH : $\text{Cosinus}=\frac{\text{Adjacent}}{\text{Hypot}\acute{\text{e}}\text{nuse}}$
    
    TOA : $\text{Tangente}=\frac{\text{ Oppos}\acute{\text{e}}}{\text{Adjacent}}$