CHAPITRE 11
Théorème de Thalès
- ÉNONCÉ DU THÉORÈME DE THALÈS1
- RÉCIPROQUE DU THÉORÈME DE THALÈS2
- AGRANDISSEMENT ET RÉDUCTION3
Utilisation du théorème
Règle
Règle
Utilisation du théorème de Thalès
➔ Pour déterminer une longueur manquante dans une configuration de Thalès, on écrit d'abord les quotiens égaux et on calcule ensuite la longueur manquante par proportionnalité.
➔
Exemple
Exemple
Consigne :
Les droites (BC) et (DE) sont sécantes en A. Les droites (BD) et (EC) sont parallèles. Calculez AE et BD. (Les unités sont en cm.) Correction :
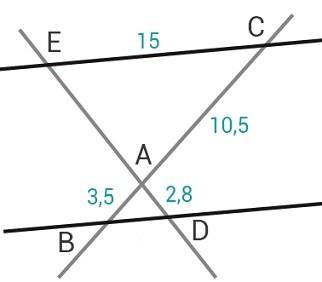 |
Énoncé du théorème
Théorème
Théorème
Théorème de Thalès
➔ (BM) et (CN) sont deux droites sécantes en A. Si les droites (BC) et (MN) sont parallèles alors :
- ABAM=ACAN=BCMN
➔
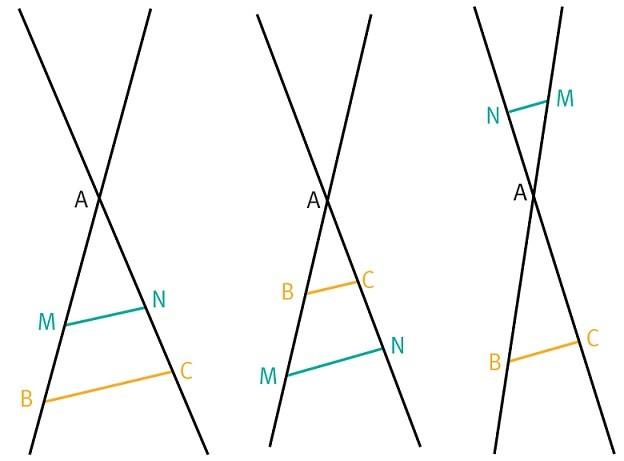
Remarque
Remarque
|
Exemple
Exemple
Consigne :
Dans les deux configurations suivantes, les droites colorées sont parallèles. Quels sont les quotients égaux ? Correction : a. IJIA=IKIB=JKAB b. GNGF=GMGE=MNEF 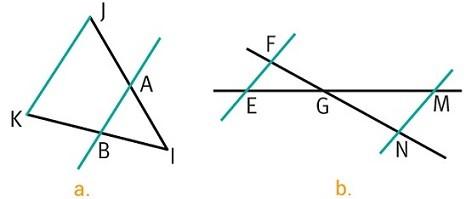 |
Utilisation des cookies
Lors de votre navigation sur ce site, des cookies nécessaires au bon fonctionnement et exemptés de consentement sont déposés.