CHAPITRE 10
Théorème de Pythagore
- THÉORÈME DE PYTHAGORE1
- RACINE CARRÉE2
- LONGUEUR D’UN CÔTÉ3
- RÉCIPROQUE DU THÉORÈME DE PYTHAGORE4
Théorème de Pythagore
Théorème
Théorème
Théorème de Pythagore
➔
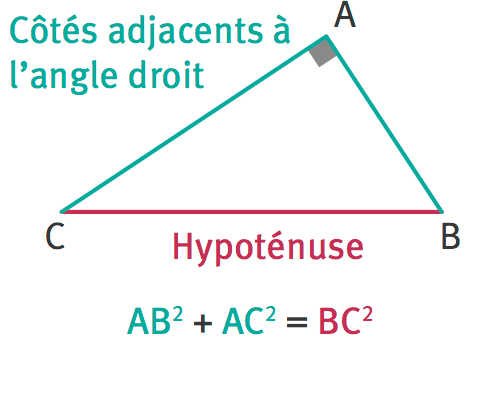
- Dans un triangle rectangle, l’hypoténuse est le côté opposé à l’angle droit.
- Si un triangle est rectangle, alors le carré de la longueur de l’hypoténuse est égal à la somme des carrés des longueurs des deux autres côtés.
- Les deux autres côtés sont appelés côtés adjacents à l’angle droit.
➔
Exemple
Exemple
Consigne :
Appliquez la formule du théorème de Pythagore au triangle DEF rectangle en D. Correction : EF2=DE2+DF2 |
Utilisation des cookies
Lors de votre navigation sur ce site, des cookies nécessaires au bon fonctionnement et exemptés de consentement sont déposés.