CHAPITRE 11
Parallélogrammes
- ANGLES ET PARALLÉLISME1
- PARALLÉLOGRAMMES QUELCONQUES2
- PARALLÉLOGRAMMES PARTICULIERS3
Parallélisme
Propriété
Propriété
Parallélismes
➔
- Si d1 et d2 sont parallèles et coupées par d, alors deux angles alternes-internes ou correspondants sont de même mesure.
- Si deux angles alternes-internes ou correspondants sont de même mesure, alors d1 et d2 sont parallèles.
- Si deux angles alternes-internes ou correspondants n’ont pas la même mesure, alors d1 et d2 ne sont pas parallèles.
➔
Exemple
Exemple
Consigne :
On considère la figure suivante dans laquelle les droites (AB) et (ED) sont parallèles. Quelle est la mesure de l’angle BCD ? Correction : Les angles EDF et ACD sont correspondants. Comme les droites (AB) et (ED) sont parallèles, EDF=ACD=45∘. Or les angles ACD et BCD sont supplémentaires, donc ACD+BCD=180∘. Donc BCD=135∘.  |
Droites parallèles
Rappel
Rappel
Droite
➔
- Deux droites qui ont un seul point commun sont dites sécantes.
- Deux droites qui ne sont pas sécantes sont parallèles.
- Deux droites qui ont deux points distincts en commun sont dites confondues. Elles ont alors tous leurs points communs.
➔
Couples d’angles
Définition
Définition
Angle adjacent
➔ Deux angles sont adjacents s’ils ont le même sommet, un côté en commun et s’ils sont de part et d’autre de ce côté en commun
➔
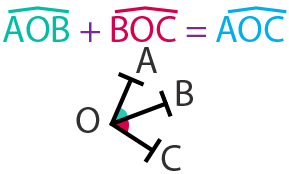
Définition
Définition
Angle supplémentaire
➔ Quand on coupe un angle plat en deux, on obtient deux angles adjacents dont la somme des mesures vaut 180∘. On dit qu’ils sont supplémentaires.
➔

Définition
Définition
Angle complémentaire
➔ Quand on coupe un angle droit en deux, on obtient deux angles adjacents dont la somme des mesures vaut 90∘. On dit qu’ils sont complémentaires.
➔
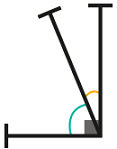
Définition
Définition
Angles opposés
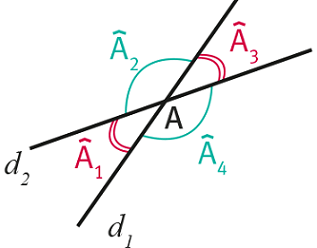
➔ Soit deux droites d et d′ sécantes en un point A :
- les angles A1 et A3 sont dits opposés par le sommet et A1=A3 ;
- de même, les angles A2 et A4 sont opposés par le sommet et A2=A4.
➔
Définition
Définition
Angles alternes-internes et angles correspondants
➔ On considère deux droites d1 et d2 coupées par une sécante d. Il existe plusieurs couples d’angles remarquables, dont :
- les angles alternes internes ;
- les angles correspondants.
➔

Exemple
Exemple
Consigne :
Dans la figure suivante, quelle est la nature des angles ?
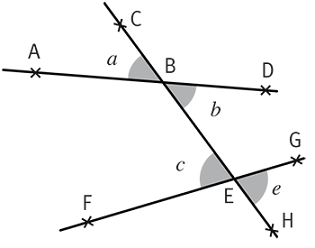 |
Utilisation des cookies
Lors de votre navigation sur ce site, des cookies nécessaires au bon fonctionnement et exemptés de consentement sont déposés.