undefined - Fiche de révision Afterclasse

CHAPITRE

0 pts

Formules et Théorèmes

À savoir refaire

Graphiques

Variations d’une fonction

Fonctions de référence

Variations d’une fonction

- Rappel
  Notion de fonction
  Une fonction est un processus qui, à un nombre $x$ , associe un unique nombre noté $f(x)$ .
  
  $f\text{ : }x\to f(x)$
- Définition
  Image et antécédent
  Si $f(x) = y$ :
  
  $y$ est l’image de $x$ par $f$ ;
  
  $x$ est un antécédent de $y$ par $f$ .
- AEnsemble de définition
  - Rappel
    Ensemble de définition d’une fonction
    L’ensemble de définition $D$ d’une fonction $f$ est l’ensemble de tous les réels $x$ qui ont une image par $f$ .
  - Exemple
    Ensembles de définition de fonctions de référence :
    
    La fonction affine $x\to f(x)=ax+b$ où $a$ et $b$ sont deux réels donnés est définie pour tout réel $x$ :
    
    son ensemble de définition est $\mathbb{R}$ .
    
    La fonction inverse $x\to f(x)=\frac{1}{x}$ n’est pas définie pour $x = 0$ :
    
    son ensemble de définition est $]-\infty;0[\cup ]0;+\infty[$ noté aussi $\mathbb{R}$ \ ${0}$ ou $\mathbb{R}^*$ .
    
    La fonction racine $x\to f(x)=\sqrt{x}$ n’est définie que pour les réels positifs :
    
    son ensemble de définition est $[0\text{ ; } +\infty[$ .
- BReprésentation graphique d’une fonction
  - Rappel
    Représentation graphique d’une fonction
    Soit $f$ une fonction définie sur $D$ .
    
    On appelle représentation graphique de la fonction $f$ l’ensemble des points $M(x;y)$ tels que $x\in D$ et $y=f(x)$ .
- CSens de variation d’une fonction
  - Rappel
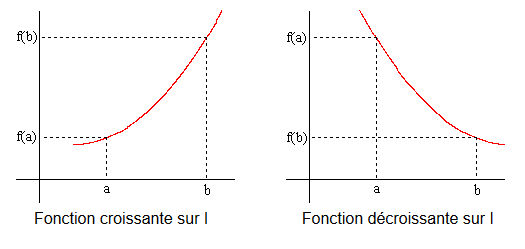
    Fonction croissante, décroissante ou constante sur un intervalle
    Soit $f$ une fonction définie sur un intervalle $I$ de $\mathbb{R}$ .
    
    $f$ est croissante sur $I$ lorsque, pour tous réels $a$ et $b$ de $I$ , si $a\le b$ alors $f(a) \le f(b)$ .
    
    $f$ est décroissante sur $I$ lorsque, pour tous réels $a$ et $b$ de $I$ , si $a\le b$ alors $f(a) \ge f(b)$ .
    
    $f$ est constante sur $I$ lorsque, pour tous réels $a$ et $b$ de $I$ , $f(a)= f(b)$ .
  - Remarque
    On peut aussi déterminer le sens de variation d’une fonction en utilisant le signe de la différence $f(b)-f(a)$ , avec $a$ inférieur ou égal à $b$ :
    
    si $f$ est croissante sur $I$ , alors $f(b)-f(a) \ge 0$ ;
    
    si $f$ est décroissante sur $I$ , alors $f(b)-f(a) \le 0$ ;
    
    si $f$ est constante sur $I$ , alors $f(b)-f(a) = 0$ .