CHAPITRE
2
AInéquation du premier degré de la forme $$ax + b < 0$$
Définition
Inéquation du premier degré de la forme ax+b<0
- Une inéquation du premier degré est de la forme ax+b<0 où a et b sont des réels.
- Résoudre cette inéquation revient à déterminer s’il existe l’intervalle solution composé des réels x tels que :
- x<a−b si et seulement si b>0 ;
- x>a−b si et seulement si b<0 .
Exemple
L’inéquation 3x+7<0 a pour solution les réels x∈]−∞;3−7[.
BInéquations produit $$A x B < 0$$ ou inéquations quotient $$A / B < 0$$
Définition
Signe de ax+b
Étudier le signe de ax+b pour tout x réel, revient à résoudre l’équation ax+b=0 et l’inéquation ax+b<0.Propriété
Signe de ax+b
Étudier le signe de ax+b pour tout x réel, revient à résoudre ax+b=0 et utiliser le sens de variation de la fonction affine f telle que f(x)=ax+b.Remarque
Pour synthétiser ces informations, nous pouvons utiliser un tableau de signe sur R.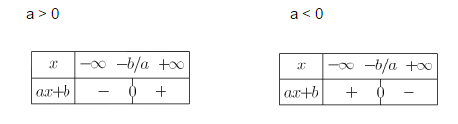
Propriété
Signe de A×B
Étudier le signe de A×B pour tout x réel, revient à étudier le signe de A et de B puis de A×B sur R.
Ces résultats sont synthétisés dans un tableau de signes.Exemple
Résoudre algébriquement l’inéquation (2x−5)(x+8)<0.
La solution est ]−8;2,5[.
Propriété
Signe de BA
- Étudier le signe de BA pour tout x réel, revient à étudier le signe de A et de B puis de BA sur R privé des valeurs qui annulent B.
- Ces résultats sont synthétisés dans un tableau de signes.
Définition
Racine de ax+b
La valeur qui annule ax+b est appelée racine de ax+b.Remarque
- Dans un tableau de signes relatif à un quotient, on précise les racines du dénominateur par une double barre.
- Nous utilisons la règle des signes pour trouver le signe d’un produit ou d’un quotient :
- le produit ou le quotient de deux termes de même signe est positif ;
- le produit ou le quotient de deux termes de signe opposé est négatif.
Exemple
Résoudre algébriquement l’inéquation 2x−3x+5>0.
La solution est ]−∞;−5[∪]23;+∞[.
Utilisation des cookies
Lors de votre navigation sur ce site, des cookies nécessaires au bon fonctionnement et exemptés de consentement sont déposés.