CHAPITRE 12
Aire et périmètre
Accueil
>
Mathématiques 6e
>
Chapitre 12 - Aire et périmètre - fiche de cours
Exercices
Fiches de cours
0 pts
Imprimer
GRAPHIQUES
1
LES NOTIONS DE PÉRIMÈTRE ET D’AIRE
2
AIRE ET PÉRIMÈTRE DE POLYGONES
3
CERCLES ET DISQUES
À SAVOIR REFAIRE
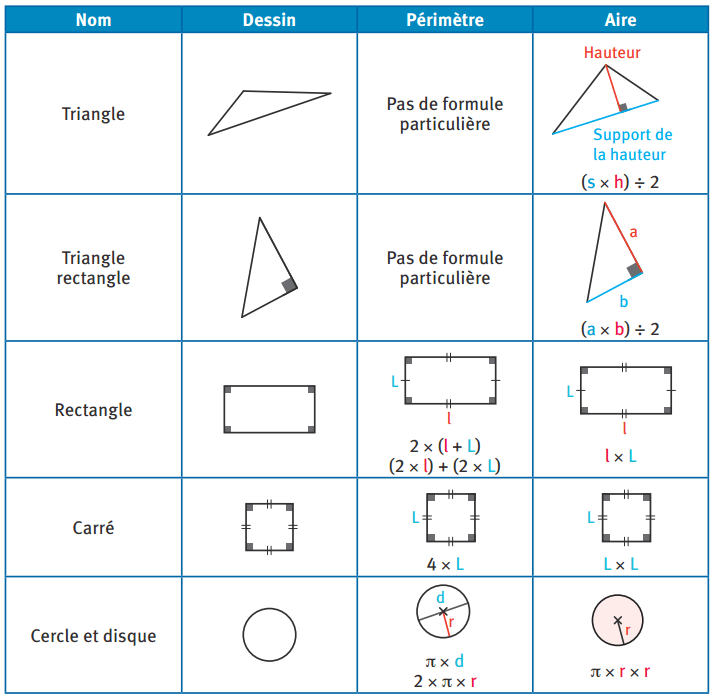
Figures du plan
M'inscrire
Me Connecter
Niveau 3ème >
Français
Histoire
Géographie
Mathématiques
SVT
Physique-Chimie
Espagnol
Mentions légales
Mes enfants
Fermer
6ème
5ème
4ème
3ème
2nde
Première
Terminale
Mon Profil
remplacer
Nom d'utilisateur
Prénom
Nom
Date de naissance
Niveau
6ème
5ème
4ème
3ème
2nde
Première
Terminale
Email
Email des Parents
Enregistrer
Changer mon mot de passe
Mon Profil
remplacer
Prénom
Nom
Matière
Allemand
Anglais
Arts plastiques
Espagnol
Français
Histoire-Géographie
Mathématiques
Musique
Philosophie
Physique-Chimie
SES
SVT
Email
Enregistrer
Changer mon mot de passe
Mon Profil
remplacer
Prénom
Nom
Email
Enregistrer
Changer mon mot de passe
Utilisation des cookies
Lors de votre navigation sur ce site, des cookies nécessaires au bon fonctionnement et exemptés de consentement sont déposés.
