CHAPITRE 10
Symétrie axiale
- TRACER LE SYMÉTRIQUE D’UNE FIGURE SIMPLE1
- AXE DE SYMÉTRIE D’UNE FIGURE2
- À SAVOIR REFAIRE
Construction du symétrique d’un segment
Propriété
Propriété
Symétrique d’une droite
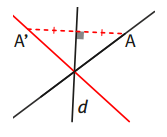
➔ Le symétrique de la droite (AB) par rapport à d est la droite (A′B′).
➔
Remarque
Remarque
Pour construire le symétrique d’une droite, on a besoin de prendre deux points sur cette droite. On peut les choisir librement ! Il vaut mieux en prendre un sur l’intersection de la droite et de l’axe de symétrie d. En effet le symétrique de ce point est lui-même !
 |
Propriété
Propriété
Symétriques de figures usuelles
➔
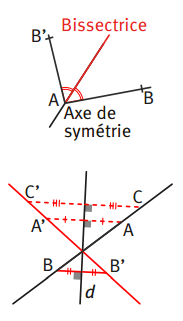
- Si A appartient à d, et si B′ est le symétrique de B par rapport à d, alors d contient la bissectrice de BAB′ !
- Le symétrique d’un segment est un segment.
- Le symétrique d’une droite est une droite.
- La symétrie axiale conserve l’alignement : si trois points A, B et C sont alignés alors leurs trois symétriques par rapport à une droite d sont alignés.
➔
Construction du symétrique d’un point
Propriété
Propriété
Symétrique d’un point
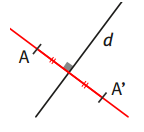
➔ Si A′ est le symétrique de A par rapport à la droite d, alors l’axe de symétrie d est la médiatrice du segment [AA′].
➔
Construction du symétrique d’un cercle
Propriété
Propriété
Propriétés de symétrie d’un cercle
➔
- Le symétrique d’un cercle est un cercle de même rayon.
- La symétrie conserve la distance : si A′ est le symétrique de A et si B′ est le symétrique de B alors AB=A′B′.
➔
Utilisation des cookies
Lors de votre navigation sur ce site, des cookies nécessaires au bon fonctionnement et exemptés de consentement sont déposés.