CHAPITRE 6
Proportionnalité
- RECONNAÎTRE DES SITUATIONS DE PROPORTIONNALITÉ1
- PRÉVOIR DANS UNE SITUATION DE PROPORTIONNALITÉ2
- À SAVOIR REFAIRE
Reconnaître des situations de proportionnalité
Définition
Définition
Grandeurs proportionnelles
➔ Deux grandeurs sont proportionnelles quand elles varient toujours dans la même proportion.
➔
Exemple
Exemple
|
Remarque
Remarque
On manipule souvent les proportions suivantes :
|
Définition
Définition
Coefficient de proportionnalité
➔ Le nombre par lequel on passe d’une quantité à l’autre s’appelle le coefficient de proportionnalité. Il peut être exprimé comme un nombre décimal, une fraction ou un pourcentage.
➔
Exemple
Exemple
Pour un paquet de fraises, on applique le coefficient de proportionnailté suivant :
 |
Remarque
Remarque
Une situation de proportionnalité est souvent représentée par un tableau de proportionnalité.
|
Exemple
Exemple
 |
Règle
Règle
Vérifier une situation de proportionnalité
➔ On peut vérifier par cette méthode si des tableaux représentent une situation de proportionnalité.
➔
Exemple
Exemple
Le tableau suivant représente-t-il une situation de proportionnalité ?
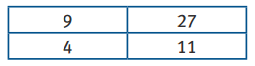 |
Utilisation des cookies
Lors de votre navigation sur ce site, des cookies nécessaires au bon fonctionnement et exemptés de consentement sont déposés.