CHAPITRE 1
Manipuler des nombres entiers
- DIVISION ENTIÈRE1
- MULTIPLES ET DIVISEURS2
- À SAVOIR REFAIRE
Division entière (ou division euclidienne)
Propriété
Propriété
Division entière (ou euclidienne)
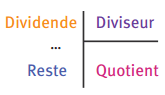
➔ Pour effectuer la division entière d’un nombre entier (le dividende) par un autre nombre entier (le diviseur), il faut trouver deux nombres entiers (le quotient entier et le reste entier) tels que :
dividende=(quotient×diviseur)+reste et le reste est plus petit que le diviseur.
➔
Remarque
Remarque
Dans une division entière, il n’y a pas de virgule !
Ex. : La division entière de 7 500 par 33 donne un quotient de 227 et un reste de 9. |
Remarque
Remarque
Le résultat d’une division entière est toujours constitué de deux nombres entiers : on dit que c’est un couple d’entiers. On ne peut l’appliquer qu’aux nombres entiers : on ne peut pas faire la division entière d’un nombre décimal par un entier !
|
Division entière ou division décimale ?
Remarque
Remarque
Lorsque l’on effectue une division de nombres entiers, il faut savoir où s’arrêter.
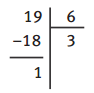 |
Remarque
Remarque
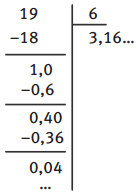 |
Utilisation des cookies
Lors de votre navigation sur ce site, des cookies nécessaires au bon fonctionnement et exemptés de consentement sont déposés.